一元二次方程复习题
初三（ ）班 学号：___________ 姓名：_____________
A组题：一、选择题
1．下列方程属于一元二次方程的是（ ）．
A.（x2-2）·x=x2 B. ax2+bx+c=0 C. x+
=5
D. x2=0
2．方程（x＋1）（x－2）＝0的根是（ ）．
Ａ．
Ｂ．
Ｃ．
Ｄ．
3．方程x（x-1）=5（x-1）的解是（ ）．
A. 1 B. 5 C. 1或5 D. 无解
4.用配方法解一元二次方程x2+8x+7=0,则方程可变形为( ).
A.(x-4)2=9 B.(x+4)2=9; C.(x-8)2=16 D.(x+8)2=57
5．下列方程中，无实数根的是（ ）．
A x2+2x+5=0 B x2-x-2=0 C 2x2+x-10=0 D 2x2-x-1=0
6．方程（x+1）（x+2）=6的解是（ ）．
A. x1=-1或x2=-2 B. x1=1或x2=-4 C. x1=-1或x2=4 D. x1=2或x2=3
7．若关于x的方程
有两个相等的实数根，则k满足（ ）
Ａ．k>1 Ｂ．k≥1 C．k=1 D．k<1
8、若
A． B、2 C、±2 D、±
9.方程x2-3x+1=0根的情况是( ).
A.有两个不相等的实数根; B.有两个相等的实数根
C.没有实数根; D.只有一个实数根
10．当代数式x2+3x+5的值为7时，代数式3x2+9x-2的值是（ ）．
A 4 B 0 C -2 D -4
11．下面是李刚同学在一次测验中解答的填空题，其中答对的是（ ）
A．若x2=4，则x＝2 B．若分式
的值为零，则x＝1，2
C．若x2+2x+k=0的一个根为1，则
D．方程x(2x－1)＝2x－1的解为x＝1
12. 用配方法将二次三项式
变形，结果是 （ ）
A.
B. 
C. 
D. 
13.党的十六大提出全面建设小康社会，加快推进社会主义现代化建设，力争国民生产总值到2020年比2000年翻两番.在本世纪的头二十年（2001年－2020年）要实现这一目标，以十年为单位计算，设每个十年国民生产总值的增长率都是
，那么满足的方程为（ ）
（A）
（B）
（C）
（D）
二、填空题
1．方程2x2-x-2=0的二次项系数是________，一次项系数是________，常数项是________．
2．关于x的方程
，当
________时为一元一次方程；当 ___________时为一元二次方程．
3．已知x2-2x-3与x+7的值相等，则x的值是______．
4．已知2是方程
的一个根，则
＝ ．
5.某种药品原来每盒售价96元，由于两次降价，现在每盒54元，则平均每次降价的百分数为 .
三．解下列方程
1．
2、 
3、 
4、
（用配方法）
5、3x2+5(2x+1)=0（用公式法）
6、
7、
8、
＝（x+1）＋56
四、解答题
1、某单位计划在长
，宽
的空地中间划出一块长方形的平地建一间仓库，使仓库四周的剩余部分一样宽，并且剩余部分的面积是总面积的
，求这个宽度。
2、 我市某企业为节约用水，自建污水净化站.7月份净化污水3000吨，9月份增加到3630吨，求这两个月净化污水量的平均每月增长的百分率.
4、 某商场销售某品牌童装，平均每天可以售出20件，每件盈利40元为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件童装降价1元，商场平均每天多售出2件，若商场平均每天要盈利1200元每件童装应降价多少元？
22、如图，有一个面积为
的长方形花园（花园的一边靠墙，墙长
），另外三边用栏杆围成，如果栏杆长
，求长方形花园的长和宽。
23．如果关于x的方程
没有实数根，试判断关于x的方程
的根的情况．
B组题
1、方程x2+ax-1=0有_______个实数根.
2、关于x的方程
是一元二次方程，则a=__________.
3、以-2和3为根的一元二次方程是_________.
4、若方程ax2+bx+c=0的一个根为-1，则a-b+c=_______．
5．若-2是关于x的一元二次方程（k2-1）x2+2kx+4=0的一个根，则k=________．
6．已知三角形的两边分别是1和2，第三边的数值是方程2x2-5x+3=0的根，则这个三角形的周长为_______．
7．若关于的一元二次方程
有两个实数根，则符合条件的一组
、
的实数值可以是=______,=________；
8．在解方程
时，如果设
，那么原方程可化为关于
的一元二次方程的一般形式是
；
10．已知x2+y2-4x+6y+13=0，x，y为实数，则x=________，y=________．
11．如果一元二次方程x2－4x＋2＝0的两个根是x1，x2，那么
x1＋x2=______________,
=_________.
12．已知x1，x2是方程x2－x－3=0的两根， 那么x12+x22的值是_________.
B4.某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元,求3月份到5月份营业额的平均月增长率.
21．现将进货为40元的商品按50元售出时，就能卖出500件．已知这批商品每件涨价1元，其销售量将减少10个．问为了赚取8 000元利润，售价应定为多少？这时应进货多少件？
3. 已知关于x的方程x2-2(m+1)x+m2=0.
(1)当m取什么值时,原方程没有实数根.
(2)对m选取一个合适的非零整数,使原方程有两个实数根,并求这两个实数根.
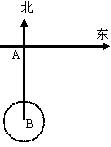
28.某军舰以20海里/时的速度由西向东航行，一艘电子侦察船以30海里/时的速度由南向北航行，它能侦察周周围50海里（含50海里）范围内的目标。如图，当该军舰行至A处时，电子侦察船正位于A处正南方向的B处，且AB=90海里。若军舰和侦察船仍按原速度沿原方向继续航行，那么航行途中侦察船能否侦察到这艘军？如果能，最早何时能侦察到？如果不能，请说明理由。
