第一章 证明(二) 单元测试卷
一、选择题:(每小题3分，共30分)
1、两个直角三角形全等的条件是（ ）
A、一锐角对应相等; B、两锐角对应相等;
C、一条边对应相等; D、两条边对应相等.
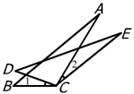
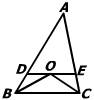
2、如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（ ）
A、SAS B、ASA C、AAS D、SSS
3、等腰三角形底边长为7，一腰上的中线把其周长分成两部分的差为3，则腰长是（ ）
A、4 B、10 C、4或10 D、以上答案都不对
4、如图，EA⊥AB，BC⊥AB，EA=AB=2BC，D为AB中点，有以下结论：
(1)DE=AC；(2)DE⊥AC；(3)∠CAB=30°；(4)∠EAF=∠ADE。其中结论正确的是（ ）
A、(1)，(3) B、(2)，(3) C、(3)，(4) D、(1)，(2)，(4)
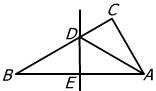
5、如图，△ABC中，∠ACB=90°，BA的垂直平分线交CB边于D，若AB=10，AC=5，则图中等于60°的角的个数为（ ）
A、2 B、3 C、4 D、5
 | |||||
 | |||||
 | |||||
(第2题图) (第4题图) (第5题图)
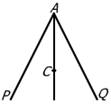
6、设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示他们之间关系的是（ ）
 |
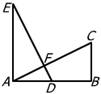
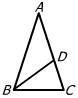
7、如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB=6cm，则△DEB的周长为（ ）
A、4cm B、6cm C、8 cm D、10cm
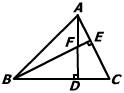
8、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）
A、30° B、36° C、45° D、70°
 | |||||||
 |  | ||||||
 | |||||||
(第7题图) (第8题图) (第9题图) (第10题图)
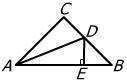
9、如图，已知AC平分∠PAQ，点B，B′分别在边AP，AQ上，如果添加一个条件，即可推出AB=AB′，那么该条件可以是（ ）
A、BB′⊥AC B、BC=B′C C、∠ACB=∠ACB′ D、∠ABC=∠AB′C
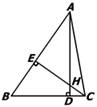
10、如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则ABC的大小是（ ）
A、40° B、45° C、50° D、60°
二、填空题:(每小题3分，共24分)
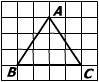
11、在方格纸上有一△ABC，它的顶点位置如图所示，则这个三角形是 三角形.
12、如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： ，使△AEH≌△CEB。
13、命题：“全等三角形的对应角相等”的逆命题是________________________________。这条逆命题是___ ___命题（填“真”或“假”）
 |  |  | |||||
 | |||||||
(第11题图) (第12题图) (第17题图) (第18题图)
14、在△ABC和△ADC中，下列论断：①AB=AD；②∠BAC=∠DAC；③BC=DC，把其中两个论断作为条件，另一个论断作为结论，写出一个真命题： _____
.
15、补全“求作∠AOB的平分线”的作法：①在OA和OB上分别载取OD、OE，使OD=OE。②分别以D、E为圆心，以 为半径画弧，两弧在∠AOB内交于点C。③作射线OC即为∠AOB的平分线。
16、在△ABC中，边AB、BC、AC的垂直平分线相交于P，则PA、PB、PC的大小关系是 .
17、如图，△ABC中，AB=6cm，AC=5cm，BC=4cm，∠ABC与∠ACB的平分线相交于点O，过点O作DE∥BC交AB于点D，交AC于点E，则△ADE的周长等于 cm.
18、如图是2002年8月在北京召开的第24届国际数学家大会的会标，它是由4个相同的直角三角形拼和而成。若图中大小正方形的面积分别为52cm2和4cm2，则直角三角形的两条直角边的和是 cm.
三、解答题
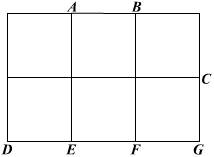
19、（本题满分7分）如图所示，它是由6个面积 为1的正方形组成的矩形，点A、B、C、D、E、F、G是小正方形的顶点，以这七个点中的任意三个为顶点，可组成多少个面积为1的三角形？请你写出所有这样的三角形.
20、（本题满分7分）如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高.
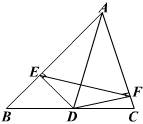求证：AD垂直平分EF.
21、（本题满分7分）阅读下题及其证明过程：
已知：如图，D是△ABC中BC边上一点，EB=EC，∠ABE=∠ACE，
求证：∠BAE=∠CAE.
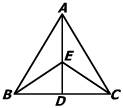证明：在△AEB和△AEC中，
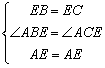
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE(第二步)
问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程。
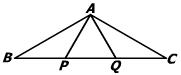22、（本题满分7分）已知：如图，P、Q是△ABC边BC上两点，且BP=PQ=QC=AP=AQ.
求∠BAC的度数.
23、（本题满分9分）某县政府准备为B、C两个村修建人畜饮水工程，取水点为A，已知AB=BC=AC，如图(1)、(2)、(3)的实线部分是三种不同的水管铺设线路设计方案，其中方案(3)的三段分别是∠BAC、∠ABC、∠BCA的平分线，设三种方案的水管长度分别是l1、l2、l3，试通过计算说明采取哪种水管铺设线路设计方案最省。
 |
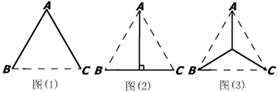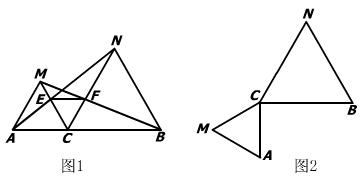
24、（本题满分9分）如图1，点C为线段AB上一点，△ACM， △CBN是等边三角形，直线AN，MC交于点F。
(1)求证：AN=BM；
(2)求证： △CEF为等边三角形；
(3)将△ACM绕点C按逆时针方向旋转900，其他条件不变，在图2中补出符合要求的图形，并判断第（1）、（2）两小题的结论是否仍然成立.（不要求证明）
 |