第一章 证明（二）数学试卷
卷Ⅰ（选择题，共20分）
请注意：
1. 答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上，考试结束，监考人员将试卷和答题卡一并收回.
2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.
一、选择题（本大题共10个小题；每小题2分，共20分）
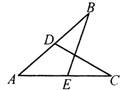
1、△ABC中，AB=AC，BD平分∠ABC交AC边于点D，∠BDC=75°，则∠A的度数为（ ）
A.35° B.40° C.70° D.110°
2、三角形的三个内角中，锐角的个数不少于( )
A.1 个 B.2 个 C.3个 D.不确定
3、适合条件∠A =∠B =
∠C的三角形一定是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形
4、用两个全等的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③正方形；④等腰三角形，一定可以拼成的图形是( )
A.①② B. ②④ C.①④ D.②③
5、如图，D在AB上，E在AC上，且∠B＝∠C，那么补充下列一个条件后，仍无法判定△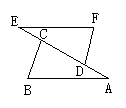
ABE≌△ACD的是( )
A.AD＝AE B.∠AEB＝∠ADC C.BE＝CD D.AB＝AC
6、如图，⊿ABC
⊿FED，那么下列结论正确的是( )
A.FC = BD B.EF∥AB C.DE = BD D.AC∥ED
7、等腰三角形的一边为4，另一边为9，则这个三角形的周长为( )
A.17 B.22 C.13 D 17或22
8、有两个角和其中一个角的对边对应相等的饿两个三角形( )
A.必定全等 B.必定不全等 C.不一定全等 D.以上答案都不对
9、以下命题中，真命题的是( )
A.两条线只有一个交点; B.同位角相等;
C.两边和一角对应相等的两个三角形全等; D.等腰三角形底边中点到两腰相等
10、面积相等的两个三角形( )
A.必定全等 B.必定不全等 C.不一定全等 D.以上答案都不对
卷Ⅱ（非选择题，共100分）
意事项：1. 答卷Ⅱ前，将密封线左侧的项目填写清楚.
2. 答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
二、填空题（本大题共5个小题；每小题2分，共10分.
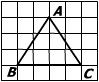
11、在方格纸上有一三角形ABC，它的顶点位置如图所示，则这个三角形是 三角形.
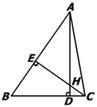
12、如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： ，使△AEH≌△CEB。
13、等腰直角三角形一条直角边的长为1cm，那么它斜边长上的高是 cm.
 | |||||
 | |||||
 | |||||
(第11题图) (第12题图) (第15题图)
14、在△ABC和△ADC中，下列论断：①AB=AD；②∠BAC=∠DAC；③BC=DC，把其中两个论断作为条件，另一个论断作为结论，写出一个真命题： ______.
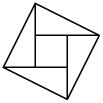
15、如图是2002年8月在北京召开的第24届国际数学家大会的会标，它是由4个相同的直角三角形拼和而成。若图中大小正方形的面积分别为52cm2和4cm2，则直角三角形的
两条直角边的和是
cm.
三、解答题（本大题共10个小题；共80分）
16. （本题共8分）
如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
（1）△BCD与△EAB是否全等？为什么？
解：∵DC⊥CA，EA⊥CA，DB⊥EB (已知)
∴∠C=∠A=∠DBE=90° ( )
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°( )
∴∠D=∠EBA ( )
在△BCD与△EAB中
∠D=∠EBA （已证）
∠C= （已证）
DB= （已知）
∴△BCD≌△EAB ( )
（2）你能说明AC=CD+AE吗？
17. （本题共6分）
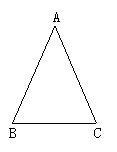
已知：如图，△ABC中，AB=AC.
(1)按照下列要求画出图形：
①作∠BAC的平分线交BC于点D；
②过D作DE⊥AB，垂足为点E；
③过D作DF⊥AC，垂足为点F.
(2)根据上面所画的图形，求证：EB=FC.
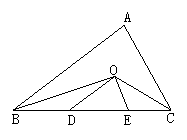
18.（本题共6分）已知，如图，O是⊿ABC的∠ABC、∠ACB的角平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若BC = 10 cm，求⊿ODE的周长.
19. （本题共6分）已知，如图⊿ABC中，∠ACB的平分线交AB于E，∠ACB的补角∠ACD的平分线为CG，EG∥BC交AC于F，EF会与FG相等吗？为什么？
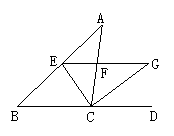
20.（本题共8分）已知，如图，AB=AC，∠A=108
，BD平分∠ABC交AC于D.
求证：BC=AB+CD.
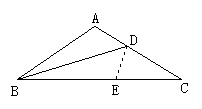
21.（本题共8分）已知，如图，⊿ABC中，∠A = 90，AB =AC，D是BC边上的中点，E、F分别是AB、AC上的点，且BE = AF，求证：ED⊥FD.
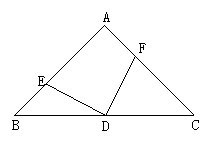
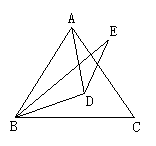
22.（本题共8分）等边三角形ABC中，D是三角形内一点，DA = DB，BE = AB，∠CBD = ∠EBD，求∠E的度数.
23.（本题共6分）在
中，
是
边上的高，
是
平分线。求
的度数。
24. （本题共12分）已知：如图，AE＝CF，∠DAF＝∠BCE，AD＝CB。
问：△ADF与△CBE全等吗？请说明理由。
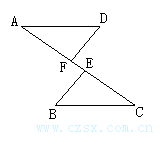
如果将△BEC沿CA边方向平行移动，可有下列３幅图，如上面的条件不变，结论仍成立吗？请说明理由。
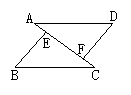
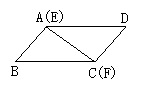
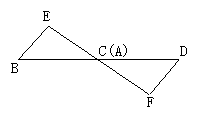
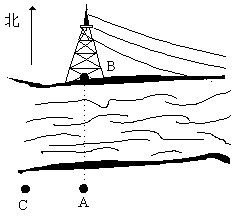
25． （本题共12分）如图：小刚站在河边的A点处，在河的对面（小刚的正北方向）的B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了20步到达一颗树C处，接着再向前走了20步到达D处，然后他左转90°直行，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他共走了100步。
（1）根据题意在原图上，画出示意图；
（2）如果小刚一步大约50厘米，估计小刚在点A处时他与电线塔的距离，并说明理由。
