第一章 证明（Ⅱ）目标检测题
班级 姓名 学号 成绩
一、判断题（每小题2分，共10分）下列各题正确的在括号内画“√”，错误的在括号内画“×”.
1、两个全等三角形的对应边的比值为1 . （ ）
2、两个等腰三角形一定是全等的三角形. （ ）
3、等腰三角形的两条中线一定相等. （ ）
4、两个三角形若两角相等，则两角所对的边也相等. （ ）
5、在一个直角三角形中，若一边等于另一边的一半，那么，一个锐角一定等于30°.（ ）
二、选择题（每小题3分，共30分）每小题只有一个正确答案，请将正确答 案的番号填在括号内.
1、在△ABC和△DEF中，已知AC=DF，BC=EF，要使△ABC≌△DEF，还需要的条件是（ ）
A、∠A=∠D B、∠C=∠F C、∠B=∠E D、∠C=∠D
2、下列命题中是假命题的是（ ）
A、两条中线相等的三角形是等腰三角形;
B、两条高相等的三角形是等腰三角形
C、两个内角不相等的三角形不是等腰三角形
D、三角形的一个外角的平分线平行于这个三角形的一边，则这个三角形是等腰三角形
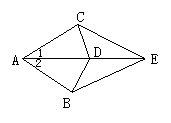
3、如图(1)，已知AB=AC，BE=CE，D是AE上的一点，则下列结论不一定成立的是（ ）
A、∠1=∠2 B、AD=DE C、BD=CD D、∠BDE=∠CDE
(1) (2) (3)
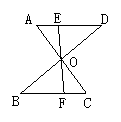
4、如图（2），已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD、BC于点E、F，则下列结论：①OA=OC;②OE=OF;③AE=CF; ④OB=OD，其中成立的个数是（ ）
A、1 B、2 C、3 D、4
5、若等腰三角形的周长是18，一条边的长是5，则其他两边的长是（ ）
A、5，8 B、6.5，6.5 C、5，8或6.5，6.5 D、8，6.5
6、下列长度的线段中，能构成直角三角形的一组是（ ）
A、
； B、6， 7， 8；
C、12， 25， 27；
D、
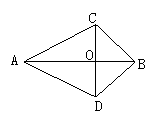
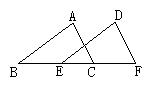
7、如图（3），AC=AD BC=BD，则下列结果正确的是（ ）
A、∠ABC=∠CAB B、OA=OB C、∠ACD=∠BDC D、AB⊥CD
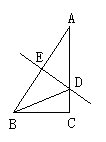
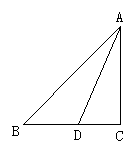
8、如图（4），△ABC中，∠A=30°，∠C=90°AB的垂直平分线交AC于D点，交AB于E点，则下列结论错误的是（ ）
A、AD=DB B、DE=DC C、BC=AE D、AD=BC
(4) (5) (6)
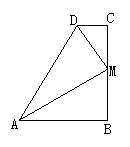
9、如图（5），在梯形ABCD中，∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，则∠MAB是（ ）
A、35° B、55° C、70° D、20°
10、如图（6），在Rt△ABC中，AD平分∠BAC，AC=BC，
∠C=Rt∠，那么，
的值为（ ）
A、
B、
C、
D、 
(7) (8) (9)
三、填空题:（每空2分，共20分）
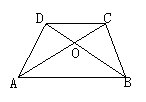
1、如图（7），AD=BC，AC=BD AC与BD相交于O点，则图中全等三角形共有___ 对.
2、如图（8），在△ABC和△DEF中，∠A=∠D，AC=DF，若根据“ASA”说明△ABC≌△DEF，则应添加条件 = . 或 ∥ .
3、一个等腰三角形的底角为15°，腰长为4cm，那么，该三角形的面积等于 .
4、等腰三角形一腰上的高与底边的夹角等于45°，则这个三角形的顶角等于 .
5、命题“如果三角形的一个内角是钝角，则其余两个内角一定是锐角”的逆命题是
.
6、用反证法证明：“任意三角形中不能有两个内角是钝角”的第一步：
假设 .
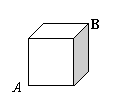
7、如图（9），一个正方体的棱长为2cm，一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物，那么它需要爬行的最短路径的长是 .
8、在Rt△ABC中，∠ACB=90°，AB=8cm， BC的垂直平分线DE交AB于D，则CD= .
9、如图（10）的(1)中，ABCD是一张正方形纸片，E，F分别为AB，CD的中点，沿过点D的折痕将A角翻折，使得点A落在（2）中EF上，折痕交AE于点G，那么∠ADG= .
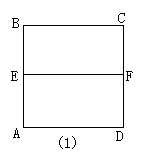
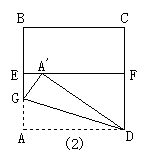
(10) (11)
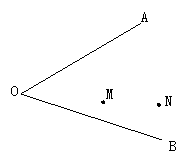
四、作图题（保留作图的痕迹，写出作法）（共6分）
如图（11），在∠AOB内，求作点P，使P点到OA，OB的 距离相等，并且P点到M，N的距离也相等.
五、解答题（5分）
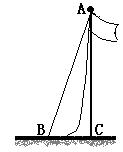如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直, 则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
六、证明题（第1，第2两小题各6分，第3小题8分，第4小题9分）
1、已知：如图，
∥
，
是
的中点，求证：是
中点.
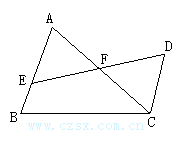
2、已知：如图，AB=AD， CB=CD，E，F分别是AB，AD的中点.求证：CE=CF .
3、如图，△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F.
求证：（1）AD⊥EF ；
（2）当有一点G从点D向A运动时，DE⊥AB于E，DF⊥AC于F，此时上面结论是否成立？
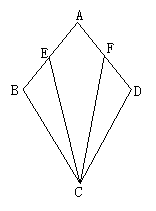
4、如图，△ABC、△DEC均为等边三角形，点M为线段AD的中点，点N为线段BE的中点，求证：△CNM为等边三角形.
第一章 证明（Ⅱ）参考答案
一、判断题 1 √，2 ×，3 ×，4 ×，5 ×
二、选择题 1、C 2、C 3、B 4、D 5、C 6、D 7、D 8、D 9、A 10、B
三、填空题 1、三；2、∠ACB=∠DFE，AB∥DE；3、4cm2 ；4、90°；5、如果两个内角是锐角，那么另一个内角是钝角；6、三角形有两个内角是钝角； 7、
；8、4cm；
9、15°.
四、作图题 （略）
五、解答题：设旗杆的高度为x米 列方程 
解 
六、证明题： 1、证明（略）
2、连结AC 先证△ABC≌△ADC 再证△AEC≌△DFC
3、先证△AED≌△AFD 得AE=AF ∠EAD=∠FAD 由等腰三角形三线合一得 AD⊥EF
（或 证AE=AF DE=DF 得A点在EF的中垂线上，D点在EF的中垂线上 ）
4、先证△ACD≌△BCE 得AD=BE ∠DAC=∠EBC 再证△ACM≌△BCN 得CM=CN
并证 ∠MCN=60°