一元二次方程测试题

　　　　　　　　 　 一元二次方程测试题

一、填空（每题4分）

1、方程的根是___________；方程的根是_____________；方程 的根是　　　　　　  ．_.

2、若方程ax²+bx+c=0的一个根为-1，则a-b+c=_______．

3．若-2是关于x的一元二次方程（k²-1）x²+2kx+4=0的一个根，则k=________．

4．已知x²+y²-4x+6y+13=0，x，y为实数，则x=________，y=________．

5．如果一元二次方程x²－4x＋2＝0的两个根是x₁，x₂，那么

x₁＋x₂=______________,=_________. x₁²+x₂²的值是_________.

6．代数式的最小值是 ______．

7．当时，与是同类项．

8.若关于的一元二次方程有实数根，则的取值范围是　　　　　　　　 。

二、选择题（每题4分）

9．已知是的三边长，那么方程的根的情况是（　　 ）

（A）没有实数根　　　　　　　　　 （B）有两个不相等的正实数根　　

（C）有两个不相等的负实数根　　　 （D）有两个异号实数根

10、用配方法解下列方程x²-2x-99=0时，正确的是（　　 ）

A．(x+1)²=100　　　　　　　　   B．(x-1)²=100

C．(x+1)²=98　　　　　　　　　 D．(x-1)²=98

11、三角形两边长分别是3和6，第三边是方程的解，则这个三角形的周长是（　　 ）

（A）11　 （B）13　　（C）11或13　 （D）11和13

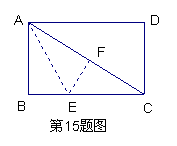12、如图，在矩形ABCD中，AB=1，BC=2，将其折叠，使AB边落在对角线AC上，得到折痕AE，则点E到点B的距离为（ ）

（A） （B）  （C） （D）

三、解下列方程（每题7分，计28分）

13、（用配方法）　　　　　  14、3x²+5(2x+1)=0（用公式法）　　　　　　　

15、　　 　　　　　　　　16、＝（x+1）＋56

四、应用题

17、（12分）某商场在“五一节”的假日里实行让利销售，全部商品一律按九销售，这样每天所获得的利润恰是销售收入的20%，如果第一天的销售收入4万元，且每天的销售收入都有增长，第三天的利润是1.25万元，

（1）　　　 求第三天的销售收入是多少万元？

（2）　　　 求第二天和第三天销售收入平均每天的增长率是多少？　　 

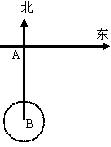
18、（12分）某军舰以20海里/时的速度由西向东航行，一艘电子侦察船以30海里/时的速度由南向北航行，它能侦察周周围50海里（含50海里）范围内的目标。如图，当该军舰行至A处时，电子侦察船正位于A处正南方向的B处，且AB=90海里。若军舰和侦察船仍按原速度沿原方向继续航行，那么航行途中侦察船能否侦察到这艘军？如果能，最早何时能侦察到？如果不能，请说明理由。

　

　　　

加试题

阅读下面的例题：

解方程

解：（1）当x≥0时，原方程化为x² – x –2=0，解得：x₁=2,x₂= - 1（不合题意，舍去）

（2）当x＜0时，原方程化为x² + x –2=0，解得：x₁=1,（不合题意，舍去）x₂= -2∴原方程的根是x₁=2, x₂= - 2

（3）请参照例题解方程