合肥二十九中学模拟测试二

合肥二十九中学模拟测试二(数学)

满分150分，时间120分

一、精心选一选（本大题共10小题，每题4分，共40分，在每题所给出的四个选项中，只有一项是符合题意的. 把所选项前的字母代号填在题后的括号内. 相信你一定会选对！）

1、的相反数为（　）

A．-3　　　　　B．3　　　　　 C．　　　　　D．

2、世界文化遗产长城总长约6 700 000，用科学记数法可表示为(　　)

A　 6.7×10⁵  B　 6.7×　C 　6.7×10⁶  D　 6.7×

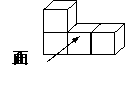
3．图中几何体的主视图是(　　)

4、已知a＜0，ab＜0，则点P（a，b）关于x轴对称的点在（　）

A．第一象限　　B．第二象限　　C．第三象限　　 D．第四象限

5、中，，若AB=2，，则的值为（　）．

A．　　　　　　 B．　　　　　　 C．　　　　　　  D．

6、某校五个绿化小组一天植树棵数分别是10、10、x、8、10，已知这组数据的众数与平均数相等，则这组数据的中位数是（　）

A、8　 B 、 9　 C、10　D、12

7、某校九（3）班的全体同学喜欢的球类运动用图4所示的统计图来表示，下面说法正确的是（　　）

A、从图中可以直接看出喜欢各种球类的具体人数；

B、从图中可以直接看出全班的总人数；

C、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；

D、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系。

8、图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（　　）

（A）25 （B）66 （C） 91（D）120

9、 小红的妈妈问小兰今年多大了，小兰说："小红是我现在的年龄时，我十岁；我是小红现在的年龄时，小红25岁。"小红的妈妈立刻说出了小兰的岁数，小兰与小红差（　　）岁。

A.10　　B.8　　　C.5　　　D.2

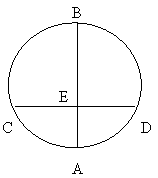
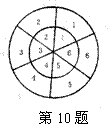10、如图，有两个同心转盘，现随意转动两转盘，两转盘静止后，恰如图情形（大转盘与小转盘的标号相对应）的概率为(　 )

A、　B、　 C、　 D、

二、细心填一填（本大题共有5小题，每空4分，共20分．请把结果直接填在题中的横线上．只要你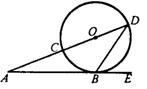理解概念，仔细运算，积极思考，相信你一定会填对的！）

11、分解因式：　　　　　　　　  ；

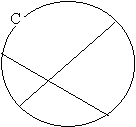
12、已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长

线交AB于点A，∠A =，则∠DBE＝_________；

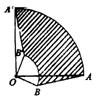13．如图，△AOB中，OA＝3cm，OB＝1cm，将△AOB绕点O逆时针旋转90°到，那么AB扫过的区域（图中阴影部分）的面积是_____________．

14、两年期定期储蓄的年利率为2.25％．国家规定，所得利息要缴纳20％的利息税．陈先生在年初存入银行一笔钱，若两年到期可得税后利息360元，则陈先生的存款数为________元．

15、自然数中有许多奇妙而有趣的现象，很多秘密等待着我们去探索！比如：对任意一个自然数，先将其各位数字求和，再将其和乘以3后加上1，多次重复这种操作运算，运算结果最终会得到一个固定不变的数R，它会掉入一个数字“陷阱”，永远也别想逃出来，没有一个自然数能逃出它的“魔掌”．那么最终掉入“陷阱”的这个固定不变的数R＝　　　　　　.

三、认真答一答（本大题共3小题，满分24分. 只要你认真思考, 仔细运算, 一定会解答正确的!）

16、计算：

17、先化简，再求值:，其中

18．如图，等腰梯形ABCD中，AD∥BC，AB＝CD，DE⊥BC于E，AE＝BE，BF⊥AE于F．请你判断线段BF与图中的哪条线段相等．先写出你的猜想，再加以证明．

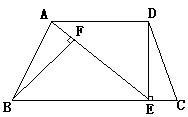（1）猜想：BF＝_____________________．

（2）证明：

四、动脑想一想（本大题共有3小题，共30分. 开动你的脑筋，只要你勇于探索，大胆实践，你一定会获得成功的！）

19、某校准备从甲、乙两家公司中选择一家公司，为毕业班学生制作一批纪念册，甲公司提出：收设计费与加工费共1500元，另外每册收取材料费5元：乙公司提出：每册收取材料费与加工费共8元，不收设计费．

　　（1）请你写出甲公司的收费（元）与制作纪念册的册数x的函数关系式；

　　（2）请你写出乙公司的收费（元）与制作纪念册的册数x的函数关系式；

　　（3）如果你去甲、乙两公司订做纪念册，你认为选择哪家公司价格优惠?

　　请写出分析理由．

20、国家课改实验区S市在2004年进行了中考评价改革：由过去的“分分计较”变为注重对学生“学业水平”的考核，下面列举了部分考试科目的相关信息。

	语文	数学	英语	物理	化学
2003年中考试卷满分	120分	120分	120分	80分	60分
2004年中考试卷满分	120分	120分	120分	100分	100分
方法：2004年采用将考生各科的中考分数转化“等级（A、B、C、D、E、F）” ，再计算各科等级的位次值之和作为毕业和高一级学校录取的重要依据	100分≤X≤120分，　 记为A等级，位次值为6 90分≤X≤99分，　　 记为B等级，位次值为5 80分≤X≤89分，　　 记为C等级，位次值为4 70分≤X≤79分，　　 记为D等级，位次值为3 60分≤X≤69分，　　 记为E等级，位次值为2 0分≤X≤59分，　　  记为F等级，位次值为1 规则：X（X为整数）为考生各科的中考分数，当两人各科的位次值之和相同时，则采用“金牌领先原则”：即谁的A等级的个数多，则谁的名次排在前；若A等级一样，则看B等级个数，依次类推…

问题1：刘明同学的五科等级为1A4B，张小思同学的五科等级为2A2B1C，马小亮同学的五科等级为1A3B1C，请分别计算三人的位次值之和，并将三人的成绩按规则由优到劣依次进行排序。

问题2：孙小伟同学参加中考，五科位次值之和为25（已知他五科等级中均没有D、E、F这三个等级），试问他五科中有几个A，几个B，几个C？

21、在“仓库世家”游戏中，游戏规则为“只要将所有木箱归位，便可过关，可以左右上下转身，推动木箱只可前进，无法后拉，按 8，2，4，6 可上下左右移动。

数字	表示
8	上移一格
2	下移一格
4	左移一格
6	右移一格

（△代表木箱，☆代表木箱应到的目的地，□代表空地，　

代表墙壁，移动一次只动一个格）其中第一关是如图一设计。移动方案为：→4→8→2→6→6→6→8→8→8。

下图为第三关，请你设计出移动方案:

方案为：→

五、研究与探索：（本大题共3小题，共36分，所有人都相信你一定能圆满的完成这最后的挑战。）

22、某医药研究所进行某一治疗病毒新药的开发，经过大量的服用试验后知：成年人按规定的剂量服用后，每毫克血液中含药量y微克（1微克=10^-3毫克）随时间x小时的变化规律与某一个二次函数y=ax²+bx+c (a≠0)相吻合，并测得服用时（即时间为0时）每毫升血液中含药量为0微克；服用后2小时每毫升血液中含药量为6微克，服用后3小时，每毫升血液中含药量为7.5微克。

（1）求出含药量y（微克）与服药时间x（小时）的函数关系式；并画出0≤x≤8内的函数的图象的示意图；

（2）求服药后几小时才能使每毫升血液中含药量最大？并求出血液中的最大含药量；

（3）结合图象说明一次服药后的有效时间是多少小时？（有效时间为血液中含药量不为0的总时间）

23、动手做一做:某校教具制作车间有等腰三角形、正方形、平行四边形的塑料若干，数学兴趣小组的同学利用其中7块恰好拼成一个矩形（如图1），后来又用它们拼出了XYZ等字母模型（如图2、图3、图4），每个塑料板保持图1的标号不变，请你参与：

（1）将图2中每块塑料板对应的标号填上去；

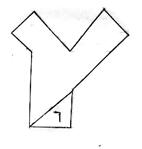
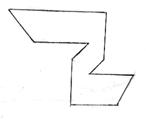
（2）图3中，点画出了标号7的塑料板位置，请你适当画线，找出其他6块塑料板， 并填上标号；（3）在图4中，找出7块塑料板，并填上标号。

　　　　　　　　　　　　　　　 　

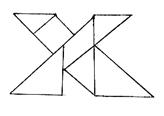
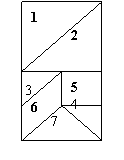
图1　　　　　　　　

图2

　　　　　　 

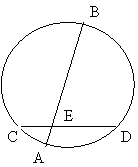
24、在一次数学实验探究课中，需要研究同一个圆中两条线段的关系问题，某同学完成了以下部分的记录，单位：cm

测 量 结果	第一次	第二次 V	第三次 B   E   D   A
AE	2.00	3.00	2.99
BE	6.01	5.00	5.00
CE	3.01	3.88	3.75
DE	3.99	3.87	4.00
AE×BE
CE×DE

（１）请你用计算器计算 AE×BE，CE×DE的值，并填入上表相应的位置。

（２）猜想对在同一个圆中，两条线段相交，被交点分成的两条线段的积有什么关系？并试着证明。

（３）利用上述结论，解决问题:AB为⊙Ｏ的弦，Ｐ是AB上一点，AB=10，PA=４，OP=５，求⊙Ｏ的半径Ｒ.