珠海市香洲区2005年初中毕业及高中阶段学校招生模拟考试
数学试卷（课改实验学校）
一、选择题（本题共5小题，每题3分，共15分）
1、
的相反数是（ ）
（A）－3 （B） 
（C） 3 （D） 
2、下列计算中，正确的是 （ ）
A．2a+3b=5ab B．a.a3=a3 C．a6÷a2=a3 D．(-ab)2=a2b2
3、在下面四种正多边形中用一种图形不能平面镶嵌的是（ ）
（A）正三角形 （B）正方形 （C）正五边形 （D）正六边形
4、图1中几何体的主视图是
5、设有12只型号相同的杯子，其中一等品7只，二等品3只，三等品2只，则从中任取一只，是二等品的概率等于（ ）
（A）
（B）
（C）
（D）
二、填空题（本题共５小题，每小题４分，共２０分）
6、函数y＝
的自变量x的取值范围是＿＿＿＿＿＿。
7、以6和2为根的一元二次方程是＿＿＿＿＿。
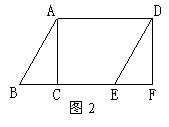
8、如图2，面积为12cm2的△ABC沿BC方向平移至△DEF位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积是＿＿＿。
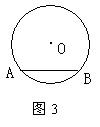
9、如图3，⊙O的半径是5cm，圆心到弦AB的距离为3cm，则弦AB的长是＿＿＿。
10、甲、乙两个同学在几次测验中，平均分都是86分，甲的方差是0.61，乙的方差是0.72，则可知成绩较稳定情况是＿＿＿＿（填甲或乙或一样）稳定。
三、解答题（本题共５小题，每小题６分，共３０分）
11、计算：（－
）2＋4×（－
）－23
12、解方程：
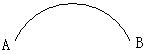
13、如图，已知：弧AB。求作：（1）确定弧AB的圆心O。
（2）过点A且与⊙O相切的直线。
（作图要求利用直尺和圆规，不写作法，但要求保留作图痕迹）
14、解下列不等式组，并把解集在数轴上表示出来。
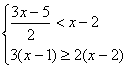
15、列方程解应用题：从甲地到乙地先下山然后过平路，某人以6千米/小时的速度下山，再以4.5千米/
小时的速度过平路，到达乙地时用了55分钟；返回时以4千米/小时的速度过平路，然后以2千米/小时的速度上山，到达甲地时用了1小时，求甲、乙两地的路程。
四、解答题：（每小题7分，共28分）
16、某汽车停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元，根据预计，解答下面的问题：
（1）写出国庆节这天停车场的收费金额y（元）与小车停放辆次x（辆）之间的函数关系式，并指出自变量x的取值范围。
（2）如果国庆节这天停放的小车辆次占停车总辆次的65%――85%，请估计国庆节这天该停车场收费金额的范围。
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合计 | a | 1.00 | |
17、为了了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，可得频率分布表.
（1）这个问题中，总体是______________________.
样本容量a=_______________.
（2）第四小组的频数b=__________，频率c=_______.
（3）若次数在110次（含110次）以上为达标，试估
计该校初三毕业生一分钟跳绳次数的达标率是多少？
（4）在这次测试中，学生跳绳次数的中位数落在哪个
小组内？
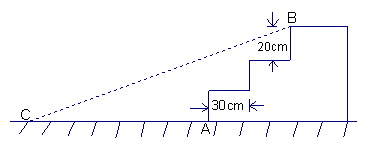18、如图，某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm.为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。 （精确到1 cm）
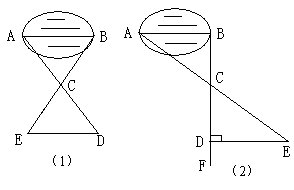19、某班同学到野外活动，为测量一池塘两端A、B的距离，设计了几种方案，下面介绍两种：
（I）如图（1），先在平地取一个可以直接到达A、B的点C，并分别延长AC到D，BC到E，使DC＝AC，BC＝EC，最后测出DE的距离即为AB的长。
（II）如图（2），先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离。
阅读后回答下列问题：
（1）方案（I）是否可行？＿＿＿＿＿＿，理由是＿＿＿＿＿＿＿＿
（2）方案（II）是否切实可行？＿＿＿＿＿＿，理由是＿＿＿＿＿＿。
（3）方案（II）中作BF⊥AB，ED⊥BF的目的是＿＿＿＿；若仅满足∠ABD＝∠BDE≠90°，方案（II）是否成立？
（4）方案（II）中，若使BC＝n·CD，能否测得（或求出）AB的长？理由是＿＿＿＿，
若ED＝m，则AB＝＿＿＿＿＿＿。
五、解答题：（每小题9分，共27分）
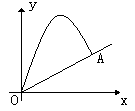20、今有网球从斜坡O点处抛出，网球的抛物线是
的图象的一段，斜坡的截线OA在一次函数
的图象的一段，建立如图所示的直角坐标系。求：（1）网球抛出的最高点的坐标。（2）网球在斜坡的落点A的垂直高度。
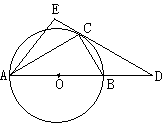21、⊙O是△ABC的外接圆，AB是直径，过点C的切线与AB的延长线相交于点D，AE⊥DC交DC于点E。（1）求证：AC是∠EAB的平分线；（2）若圆的半径为3，BD＝2，DC＝4，求AE和BC。
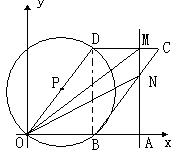22、如图，四边形OBCD为平行四边形，OD＝2，∠DOB＝60°，以OD为直径的⊙P经过点B，N为BC上任意一点（与B、C不重合），过N作直线MN⊥x轴，垂足为A，MN交DC于M，设OA＝t，OMN的面积为S。
（1）求出D、B、C点的坐标和过B、C两点的一次函数的解析式。
（2）求S与t之间的函数关系式及t的范围。
（3）当S＝
时，试判定直线MN与⊙P的位置关系。
部分参考答案
17、（1）初三毕业班学生一分钟跳绳次数的全体. a=100.
（2）b=39. c=0.39.
（3）达标率为93%.
（4）落在第3小组.
18、AC的长度为222cm