九年级数学周测试
-----圆心角、圆周角、确定圆的条件
一、选择题（36分）
1、下列说法不正确的是 （ ）
A 圆周角的度数等于所对弧的度数的一半
B 圆是中心对称图形，也是轴对称图形
C 垂直于直径的弦必被直径平分
D 劣弧是大于半圆的弧
2、以直角坐标系的原点为圆心作一个半径为5的圆，则以下各点中：J（3，3）、K（0，5）、L（
，－4）、M（4，3）、N（－1，6），在圆外的点有 （ ）
A J和L B L和N C K和M D J和N
3、在⊙O中，AB、AC是互相垂直的两条弦，AB=8，AC=6，则⊙O的半径为 （ ）
A 4 B 5 C 8 D 10
4、下列所述图形中对称轴最多的是（ ）
A 圆 B 正方形 C 正三角形 D 线段
5、平面上有4个点，它们不在同一直线上，过其中3个点作圆，可以作出不重复的圆n个，则n的值不可能为 （ ）
A 4 B 3 C 2 D 1
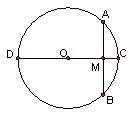
6、如图，⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD于M，且DM∶MC=4∶1，则AB的长是 （ ）
A 2
B 8 C 16 D 
第6题
第7题
第9题
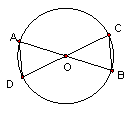
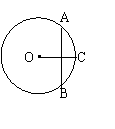
7、如图，AB、CD为⊙O直径，则下列判断正确的是 （ ）
A AD、BC一定平行且相等
B AD、BC一定平行但不一定相等
C AD、BC一定相等但不一定平行
D AD、BC不一定平行也不一定相等
8、若⊙A的半径为5，圆心A的坐标是(3，4)，点P的坐标是(5，8)，你认为点P的位置为（ ）
A 在⊙A内 B 在⊙A上 C 在⊙A外 D 不能确定
9、如图，两枚大小相同的硬币，一枚固定不动，另一枚绕其边缘滚动(无滑动)，当运动硬币滚动到原来位置(第一次重合)时，运动硬币自转了______圈.
A 1 B 2 C 3 D 4
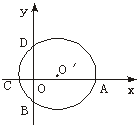
10、如图10，在平面直角坐标系中，⊙O′与两坐标分别交于A、B、C、D四点，已知：A(6，0)，B(0，－3)，C(－2，0)，则点D的坐标为（ ）
A (0，2) B (0，3) C (0，4) D (0，5)
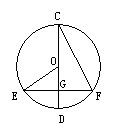
11、如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°,则∠DCF等于（ ）
A 80° B 50° C 40° D 20°
12、点P为⊙O内一点，且OP＝4，若⊙O的半径为6，则过点P的弦长不可能为 （ ）
A 
B 12
C 8
D 10.5
二、填空题（24分）
13、A、B是半径为10cm的⊙O上的不同两点，则弦AB的长度最长为 cm。
14、已知AB是⊙O的弦，且AB=OA，则∠AOB＝ 度。
15、在⊙O中，弦AB=9，∠AOB＝120°，则⊙O的半径为 。
16、如图，点A、B、C在⊙O上，∠C＝150°，则∠AOB＝ 。
第16题 第17题 第18题
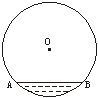
17、如图⊙O的直径为12cm,弦AB垂直平分半径OC，那么AB=
18、为改善市区人民生活环境，市建设污水管网工程，某圆柱型水管的直径为100 cm，截面如图18，若管内污水的面宽AB=60 cm，则污水的最大深度为_____ cm.
三、解答题（90分）
19、如图，四边形ABCD中，∠A=130°，∠B=90°，∠C＝50°，则过四点A、B、C、D能否画一个圆？若能，请画出这个圆，请简单说明理由。（10分）
|
|
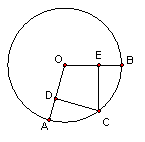20、如图，点C是AB上的点，CD⊥OA于D，CE⊥OB于E，若CD=CE。求证：点C是AB的中点。（10分）
|
|
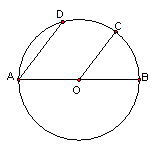21、如图，AB是⊙O的直径，且AD∥OC，若AD的度数为80°。求CD的度数。（10分）
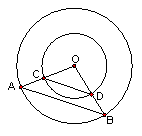
22、点O是同心圆的圆心，大圆半径OA、OB交小圆于点C、D。求证：AB∥CD（10分）
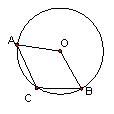
23、如图①，点A、B、C在⊙O上，连结OC、OB：
⑴ 求证：∠A=∠B+∠C；（6分）
⑵ 若点A在圆上移动（不与点B、C重合），请分析∠A、∠B、∠C三者之间的数量关系。（写出结论即可，6分）
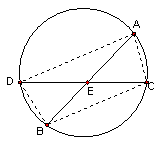24、AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD。则以下结论中：①AE=EC、②AD=BC、③BE=EC、④AD∥BC，正确的有
。（写出所有正确的结论）（6分）试证明其中一个结论。（8分）
25、如图，一座弧形桥的跨度AB为40米，桥离水面最大距离CD为10米，一条水面以上宽度为30米，高度为6米的船能否通过这座桥？（12分）
 |
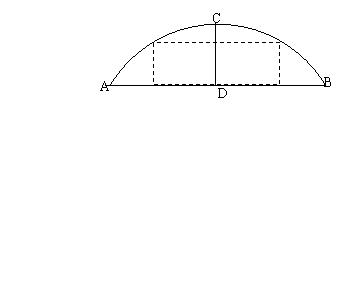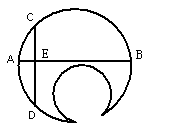
25、如图，这是某公司的产品标志，它由大小两个圆和大圆内两条互相垂直的弦构成。现在只有一把带刻度的直尺，请设计一个可行的方案，通过测量，结合计算，求出大圆的半径r。（方案中涉及到的长度可用字母a、b、c等来表示）（12分）
