2005—2006学年第一学期初三年级
期末考试数学试卷
总分 100分 考试时间 ：90 分钟
一、填空题（共10题，每题3分，共30分.）
1.
的根是
2.正方形的对角线长为
，则面积为_______
3．已知菱形ABCD的周长为
，BD＝
，则这个菱形的面积是
．
4、若
是x的反比例函数，则k=_________
5、矩形的宽为4cm，两对角线相交成60°角，该矩形的长为_________.
6.、已知等腰三角形的一个角为80°，则其顶角为_________.
7．在△ABC中，∠C＝90°，若BC＝4，sinA=
，则AC的长是
8．二次函数
的对称轴是
9、 双曲线
经过点（2 ，―3），则k = .
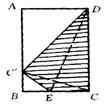
10．如图，矩形ABCD的长、宽分别为5和3，将顶点C折过来，使它落在AB上的C/点（DE为折痕），那么，阴影部分的面积是 .
二、选择题（共5题，每题3分,共15分.请把正确答案的代号填入下表中.）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
11、若将函数y=2x2的图象向右平行移动1个单位，再向上平移3个单位，可得到的抛物线是（ ）
A y=2(x-1)2-3 B y=2(x-1)2+3 C y=2(x+1)2-3 D y=2(x+1)2+3
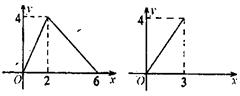
12、图4所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时指向奇数的概率为（ ）
A．
B．
C．
D．
 | |||||
 |  | ||||
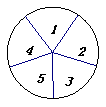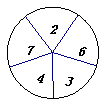（ 第13题图）
13..如图，在平行四边形ABCD中，AC=4，BD=6，P是BD上的任一点，过P作EF∥AC，与平行四边形的两条边分别交于点E，F. 设BP=x，EF=y，则能反映y与x之间关系的图象为（ ）
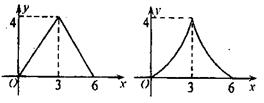
A B C D
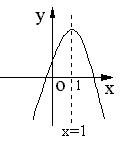14．二次函数y=ax2+bx+c的图象如图所示，对称轴x=1，下列结论中，正确的是（ ）
A．ac>0 B．b<0
C．b2-4ac<0 D．2a+b=0
15、如果k＜0，那么下列说法中正确的是（ ）
A.函数y＝kx中，y随着x的增大而增大
B.函数 
的图象的两个分支分别位于第一、三象
C.抛物线y＝(x+k)
的对称轴是直线x＝-k
D.直线y＝kx-k经过第二、三、四象限
三．画图题（4分）：
16. 旗杆、树和竹杆都垂直于地面且一字排列，在路灯下树和竹杆的影子的方位和长短如图所示. 请根据图上的信息标出灯泡的位置（用点P表示），再作出旗杆的影子（用线段AB表示）. （不写作法，保留作图痕迹）
四．解答题（满分27分.）
17．解方程 x
- 3 x + 1= 0 （4分）
解：
18 . 计算（每小题4分，共8分）
(1)
（4分）
解：
(2) （4分）在
中，
，∠A的平分线 AD =
16 ，求AB的长 。
解：
 |
19. （5分）抛物线y＝ax2＋bx＋c如右图所示,求它关于y轴对称的抛物线的解析式;并写出它的对称轴和顶点坐标。
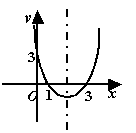解：
20. （6分）如图，已知一次函数
的图象与反比例函数
的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是－2，求：
（1）一次函数的解折式；
（2）△AOB的面积。
解：
21. （5分）为申办2010年冬奥会，须改变哈尔滨市的交通状况。在大直街拓宽工程中，要伐掉一棵树AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°. 问：距离B点8米远的保护物是否在危险区内？
四．几何证明：（每小题5分，共10分.）
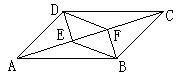
22. 如图：平行四边形ABCD中，DE⊥AC于E，BF⊥AC于F，
求证：DF=BE。
23.如图，在△ABC中，AB=4，AC=3，BC=5，DE是BC的垂直平分线.
(1) 求证：△ABC为直角三角形；
(2)
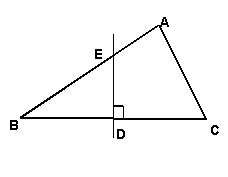求DE的长.
五. （24题5分，25题8分）
24、某商店经销一种销售成本为每件40元的T恤，根据市场分析，若按每件50元售出，一个月能销售500件，销售单价每涨1元，月销售量就减少10件.请解答以下问题
(1)当销售单位定为每件55元时，月销售量和月销售利润各是多少？
(2)设销售单价为每件
元，月销售利润为
元，求与之间的函数关系式.
(3)商店想在月销售成本不超过10000元的情况下，使得月销售利润达8000元，销售单价应定为多少才合适？
| |
.
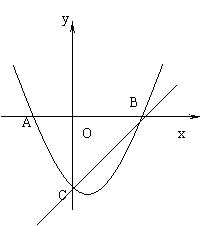
25.如图所示，二次函数y=ax2+bx+c的图象与x轴交于A点和B点(A. B分别位于原点O的两侧)，与y轴的下半轴交于c点，且tan∠OAC=2,AB=CB=5.
(1) 求直线BC和二次函数的解析式；
(2) 直线BC上是否存在这样的点P，使⊿PAB和⊿OCB相似？若存在，求满足条件点P的坐标；若不存在，请说明理由。
 |
答案:
一.
1).x1=-1,x2=2; 2).4 ; 3)96 cm2; 4) 1 ;5)4
cm; 6)800或200; 7)2
; 8) x=-3;
9) –6; 10) 
二. B B A D C
三. 略
四.
17 
18 (1) 2; (2) AB=16
19 原解析式 y=x2-4x+3 对称轴为直线x= 2 顶点坐标 ( 2,-1)
与 y轴对称的抛物线的解析式 y=x2+4x+3
20. 一次函数 y= -x+2
面积 6
21.
AB=4>8 无危险
22. 略
23. (1) 略
(2)DE=
五. 24. (1) 450件 6750元
(2 ) y= -10x2+1400x-40000
(3) 80元
25
(1) 
(2) 两个 