2004年的填空题
1、如图，AD、AE是正六边形的两条对角线，不添加任何辅助线，请写出两个正确的结论：（1）
__________________；
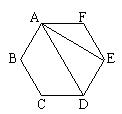
（2） ______________。
（只写出两个你认为正确的结论即可）
2、已知函数：（1）图象不经过第二象限；（2）图象经过（2，-5），
请你写出一个同时满足（1）和（2）的函数关系式：
________________________________________________.
3、观察下面一列数：-1，2，-3，4，-5，6，-7，．．．，将这列数排成下列形式
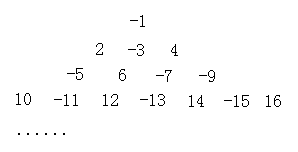
按照上述规律排下去，那么第10行从左边第9个数是_________________________
4、已知（x1,y1），(x2,y2)为反比例函数
图象上的点，当x1＜x2＜0时,y1＜y2,则k的一个值可为
（只需写出符号条件的一个k的值）
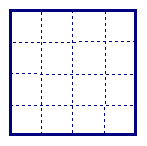
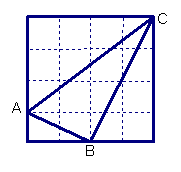
5、正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等。
.
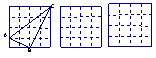
6、要使一个菱形成为正方形，则需增加的条件是 （填上一个正确的条件即可）。
7、有两块同样大小且含角60°的三角板，把它们相等的边拼在一起（两块三角板不重叠），可以拼出 个四边形。
8、观察下列等式9-1=8
16-4=12
25-9=16
36-16=20
…………
这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律为
.
9、给出一个正方形，请你动手画一画，将它剖分为n个小正方形。那么，通过实验与思考，你认为这样的自然数
可以取的所有值应该是_________________
10、扑克牌游戏
小明背对小亮，让小亮按下列四个步骤操作：
第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；
第二步 从左边一堆拿出两张，放入中间一堆；
第三步 从右边一堆拿出一张，放入中间一堆；
第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.
这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .
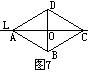11、如图7，直线
是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC⊥BD；③AO=OC；④AB⊥BC，其中正确的结论有_________。
12、观察下列等式：
，
，
，
，…，由此可判断
的个位数字是_______。
13、如图4,⊙O直径CD与弦AB（非直径）交于点M，添加一个条件：______，就可得到点M是AB的中点.
14、学生李军在一次数学活动课中，将一圆形纸板，经过多次剪裁，把它剪裁成若干个扇形.操作要求：第1次剪裁，将画形纸板等分成4个扇形；第2次剪裁，将上次得到的扇形中的一个再等分成4个扇形；以后按第2次剪裁的做法进行下去.请你结合他的剪裁过程填表：
| 剪裁次序 | 1 | 2 | 3 | … | 10 |
| 所得扇形总个数 | 4 | 7 | … |
15、科学发现：植物的花瓣、萼片、果实的数目以及其他方面的特征，都非常吻合于一个奇特的数列——著名的裴波那契数列：1，1，2，3，5，8，13，21，34，55，……仔细观察以上数列，则它的第11个数应该是 .
16、如果四边形
满足条件： ，那么这个四边形的对角线
和
相等．（只需填写一个你认为适当的条件即可）
17、请任意写一个能在实数范围内分解因式的二次三项式 （该二次三项式的字母、系数不限）
18、已知二次函数
的图象交
轴于
、
两点，交
轴于
点，且
是直角三角形，请写出符合要求的一个二次函数的解析式：____________
．
19、.观察下列由棱长为1的小立方体摆成的图形，寻找规律：
如图①中:共有1个小立方体，其中1个看得见，0个看不见；如图②中:共有8个小立方体，其中7个看得见，1个看不见；如图③中:共有27个小立方体，其中19个看得见，8个看不见；……，则第⑥个图中，看不见的小立方体有______个.
 |
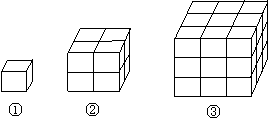20、观察下列各式：
……请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来
是_____________________.
21、用计算器探索：按一定规律排列的一组数：
，
，
，…，
，
如果从中选出若干个数，使它们的和大于0.5，那么至少要选________个数
22、正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等。
23、若a、b都是无理数，且a＋b＝2，则a、b的值可以是______________________.
(填上一组满足条件的值即可)
24、水平放置的正方体的六个面分别用“前面、后面、上面、
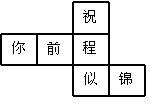下面、左面、右面”表示.如右图,是一个正方体的平面
展开图,若图中的“似”表示正方体的前面, “锦”
表示右面, “程”表示下面.则“祝”、 “你”、
“前”分别表示正方体的______________________.
25、.如图,请写出等腰梯形
∥
特有而一般
梯形不具有的三个特征:_________;_________;
__________.
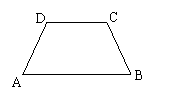26、如图，□ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的
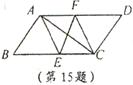图形，请添加一个条件，使四边形AECF为菱形，则添加的一个
条件可以是 (只需写出一个即可.图中不能再添加
别的“点”和“线”).
27、用边长为1cm的小正方形搭如下的塔状图形，则第n次所搭图形的周长
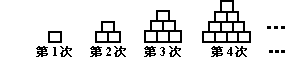是_________ cm（用含n的代数式表示）．
28、观察下面一列数，按某种规律在横线上填入适当的数，并说明你的理由.
，
，
， ，
，…你的理由是_______________.
29、某些植物发芽有这样一种规律：当年所发新芽第二年不发芽，老芽在以后每年都发芽.发芽规律见下表（设第一年前的新芽数为a）
| 第×年 | 1 | 2 | 3 | 4 | 5 | … |
| 老芽率 | a | a | 2 a | 3 a | 5 a | … |
| 新芽率 | 0 | a | a | 2 a | 3 a | … |
| 总芽率 | a | 2 a | 3 a | 5 a | 8 a | … |
照这样下去，第8年老芽数与总芽数的比值为_______（精确到0.001）
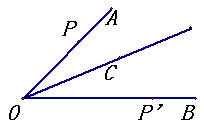30、如图，已知点C是∠AOB的平分线上一点，点P、P’分别在边
OA、OB上。如果要得到OP=OP’，需要添加以下条件中的
某一个即可，请你写出所有可能的结果的序号为____________
①∠OCP=∠OCP’； ②∠OPC=∠OP’C；
31、观察按下列顺序排列的等式：
……
猜想：第个等式（为正整数）用表示，可以表示成 ；
32、写出一个一次函数的解析式，使它的图象与x轴的夹角为
.这个一次函数的解析式是：__________.
33、按照一定顺序排列的一列数叫数列,一般用a1，a2，a3，…，an表示一个数列，可简记为{an}.现有数列{an}满足一个关系式：an+1=
-nan+1,(n=1,2,3,…,n),且a1=2.根据已知条件计算a2,a3,a4的值，然后进行归纳猜想an=_________.（用含n的代数式表示）