上学期华师大九年级期末考试卷华师大版

2005—2006上学期华师大九年级期末考试卷

数　学　试　题

（满分150分，时间120分钟）

亲爱的同学们，准备好了吗？让我们一起对初三所学的数学知识做个小结吧！我们希望通过这次测试，了解你们对初三数学的掌握程度，相信你能认真解答好！　　

题号	一	二	三	四	五	六
得分

一、 选择题:(将下列各题唯一正确答案代号A、B、C、D填到题后的括号内。每题4分,共40分)

1、一元二次方程x²－4＝0的解是　　　　　　　　　　　　　　　　　　  （　　 ）

A、x＝2　　 B、x₁＝2 ，x₂＝－2　 C、x＝－2　　D、x₁＝ ，x₂＝－

2、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年（2001年～2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的平均增长率都是x，那么x满足的方程为　　　　　　　　　　 　　　　　　　　　　　　　　(　　　 )

A、（1＋x）²＝2　　 B、（1＋x）²＝4　 C、1＋2x＝2　　D、（1＋x）＋2（1＋x）＝4

3、到△ABC的三个顶点距离相等的点是△ABC的　　　　　　　　　　　　 （　　 ）

A、三条中线的交点　　 B、三条角平分线的交点　 C、三条高线的交点　

D、三条边的垂直平分线的交点

4、关于x的一元二次方程（a－1）x²＋x＋a²－1＝0的一个根是0，则a的值为 （　　 ）

A、1　　B、－1　　C、1或－1　 D、

5、已知⊙O₁、⊙O₂的半径分别为2和5，O₁O₂＝7，则

⊙O₁和⊙O₂的位置关系是（　　）

A、外切　　B、内切　　C、相交　　D、相离

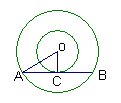6、如图，以O为圆心的同心圆中，大圆的弦切小圆于点C，两圆的半径分别是5cm和3cm，则AB=(　　)

　A、8cm　　 B 、4cm　　C 、cm　　 D 、cm

7、试验中学初三年级进行了一次数学测验，参考人数共

540人，为了了解这次数学测验成绩，下列所抽

取的样本中较为合理的是　　　　　　　　　　　　　　　　  （　　）

A、抽取前100名同学的数学成绩　　B、抽取各班学号为3号的倍数的同学的数学成绩

C、抽取（1）、（2）两班同学的数学成绩　　　 D、抽取后100名同学的数学成绩

8、纳米（nm）同千米、米、厘米一样，是长度计量单位，它是英文nanometer的中译英的

简称，1纳米是十亿分之一米，中科院物理研究员彭练矛在单壁碳纳米管的电子显微镜研究

中，发现了直径为0.33纳米的碳纳米管，用科学计数法表示，该直径为（　　　）

（A）0.33×10^-9米　　（B）0.33×10^-10米　　（C）3.3×10^-9 米　 （D）3.3×10 ^-10米

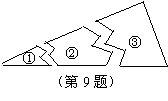9.小亮不慎将一块三角形玻璃打碎为三块(如图)，他准备带着碎片到玻璃店去配一块与原来一样的三角形玻璃，最简便的带法应该是(　).

(A)只带上碎片③　　　 (B)带上碎片①和②

(C)只带上碎片① 　　　(D)只带上碎片②

10、某商店举办有奖销售活动，购货满100元者发对奖券一张，在10000张奖券中，设特等奖1个，一等奖10个，二等奖100个。若某人购物满100元，那么他中一等奖的概率是 （ 　　）

A、 　　B、　　  C、　　　 D、

二、填空题：（每小题4分，共20分）

11、=_____时，分式没有意义。

12、命题：“过一点有且仅有一条直线垂直于已知直线”的题设是__________，结论是___________.

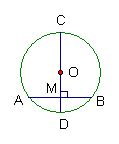
13、如图，CD是⊙O的直径，AB是弦，CD⊥AB，交AB于M，

则可得出AM=MB，弧AC=弧BC等多个结论，请你按现在的图形

再写出两个与以上不同的结论_____________.（可自连线段）

14、若，则x的值是______________。

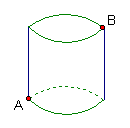15、如图，一个圆柱体高为20cm，底面半径为cm，在圆柱体的底面A点处有一只蚂蚁，想吃到与A相对的上底面B点处的一粒砂糖，这只蚂蚁从A点出发沿着圆柱体的曲面爬到B点，最短路程为_________.

三、解答题（本大题共4小题，每小题8分，共32分. 解答需写出必要的步骤和过程）

16、请将代数式尽量化简，再选择一个你最喜欢的数代入求值： 

17、 解方程： ＝

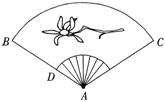
18、如图，扇形纸扇完全打开后，外侧两竹条AB、AC的夹角为120°，AB长为30cm，贴纸部分BD长为20cm，求贴纸部分面积.

19、如图，某镇要在进入镇区的道路叉口的三角地处建造一座镇标雕塑，树立其文明古镇的形象。要求使塑造中心到道路三边的距离相等，请你在图中用直尺和圆规作出这个中心位置。

（不写作法，但应保留作图痕迹并写出结论）

四、（本大题共三小题，每小题10分，共30分）

20、张师傅从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为15米³的无盖长方体运输箱。且此长方体运输箱底面的长比宽多2米，现已知购买这种铁皮每平方米20元钱。问张师傅购回这张矩形铁皮共花了多少元钱？

21、已知△ABC内接于⊙O，过点A作直线EF。

（1）（4分）如图甲所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）：（1）_______；（2）__________。

　

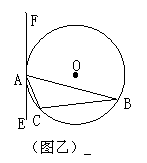
（2）（6分）如图乙所示，若AB不是⊙O的直径而是弦，且∠CAE =∠B，EF是⊙O的切线吗？试证明你的判断。

22、交通信号灯，又称红绿灯，至今已有一百多年的历史。“红灯停，绿灯行”是我们生活中必须遵守的交通规则，这样才能保障交通的顺畅和行人的安全。下面这个问题你能解决吗？

小刚每天骑自行车上学都要经过三个安装有红绿灯的路口，假如每个红灯和绿灯亮的时间相同，那么，小刚从家随时出发去学校，他至少遇到一次红灯的概率是多少？不遇到红灯的概率是多少？（请用树状图分析）

五、（本题满分14分）

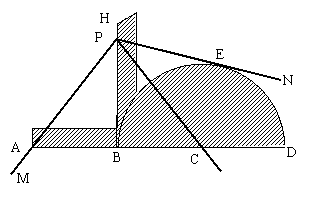
23、 三等分角仪——把材料制成如图所示的阴影部分的形状，使AB与半圆的半径CB、CD相等，HB垂直于AD，这便做成了“三等分角仪”．如果要把∠MPN三等分时，可将三等分角仪放在∠MPN上，适当调整它的位置，使HB通过角的顶点P，使A点落在角的PM边上，使角的另一边与半圆相切于E点，最后通过B、C两点分别作两条射线PB、PC，则∠MPB=∠BPC=∠CPN．请用推理的方法加以证明．

六、（本题满分14分）

24、某校九年级（一）班到校外上一节测量课，为测量一池塘两端A、B的距离，同学们设计出以下几种方案：

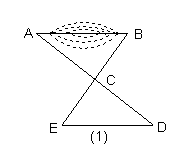
（Ⅰ）如图（1）所示，先在平地取一个可直接到达A、B点的点C，再连结AC、BC，并延长AC至D，BC至E，使得DC=AC，EC=BC，最后测出DE的距离即是AB之长。

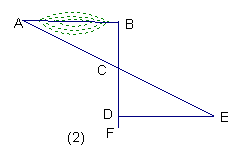
（Ⅱ）如图（2）所示，选过B点作AB的垂线BF，再在BF上取C、D两点，使得BC=CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出了DE的长即是AB的长。

　

回答下列问题：

方案（Ⅰ）是否可行？答：______，理由是___________________；

方案（Ⅱ）是否可行？答：______，理由是___________________；

方案（Ⅱ）中作BD⊥AB，ED⊥BF的目的是：_____________，若仅满足∠ABD=∠BDF≠90°，方案（Ⅱ）的结论是否成立？答：______理由是________________；

方案（Ⅱ）中若使BC= n·CD，能否测出（或求出）AB的长？答：________；理由是______________；若ED= m，则AB=_________。

温馨提示:

祝贺你做完了考题,请你再仔细检查一遍,看看有没有错的,漏的,别留下什么遗憾哦!

九年级数学试题参考答案及评分标准

说明：

(1)参考答案供阅卷教师参考，学生答题时，只要解题思路方法正确，答案符合题意，虽与参考答案有出入，均可给分.

(2)本试卷中的开放性题目，由于答案不唯一，学生答案符合题意的，同样给分.

(3)解答题右端所注的分数，表示学生正确做到这一步应得的累加分数；

一、选择题（每小题4分，共40分）

题号	1	2	3	4	5	6	7	8	9	10
答案	B	B	D	B	A	A	B	D	A	B

二、填空题（每小题4分，共20分）

11、3；　　12、过一点的直线垂直于以知直线、这样的直线有且只有一条；　　 13、AC=BC、弧AD=弧BD；　　14、x=2；15、10cm

三、16. 解： .(1－)

＝.　 …………………………………………………3分

＝x+2　……………………………………………………………………5分

代入求值（答案不唯一，但x不能取0、1。）…………………………………8分

17. 解：…………………………………………………3分

 ………………………………………………………………6分

x=3　

经检验：x=3是原方程的解。………………………………………………8分

18.解：S_贴纸=π AB²-πAD²…………………………………4分

　　　　  =π（AB² -AD²）　　　 …………………………………6分

　　　　  =π（30²-10²）　　　　 …………………………………7分

　　　　  =πcm²　　　　　　　 …………………………………8分

19.无作图痕迹不给分，作出两角或三角中垂线给6分，写出结论给2分。

20解：这种运输箱得底部宽为x米

根据题意，得x(x+2)×1＝15……………………………………………………4分

化简，得x²+2x-15=0

解得x₁=-5(不合题意，舍去。) ，x₂=3

所以这种运输箱得底部长为5米，宽为3米…………………………………7分

由长方体的展开图知，要购买的矩形铁皮面积为：

（5+2）×（3+2）＝35（米²）…………………………………………………9分

所以张师傅购回这张矩形铁皮要花35×20＝700元钱。………………………10分

21、（1）AB⊥EF或∠CAE=∠B或∠BAF=90°或∠BAF=∠BAE（4分）

　 （2）证明：连结AO并延长AO交⊙O于点D，连接CD （1分）

　　　　因为∠CAE=∠B（已知），

　　　　而∠B=∠D（同弧所对的圆周角相等）

　　　　所以∠CAE=∠D（等量代换）（2分）

　　　　因为AB为⊙O直径，（作图）

　　　　所以∠ACD=90°（直径所对的圆周角是直角）（3分）

　　　　所以∠CAD+∠D=90°（直角三角形两锐角互余）  （4分）

　　 故∠CAD+∠D=90°（等量代换）（5分）

　　 即AD⊥EF。

　　 所以EF为⊙O切线，（经过半径外端点且垂直于这条半径的直线是圆的切线（6分）

22、解：

　　　　　　　　　　　　　　　　　　　  家

第一个路口　　　　　　　　 红灯　　　　　　　　　　　 绿灯　（1分）

第二个路口　　　　　 红灯　　　　 绿灯　　　　  红灯　　　　绿灯------------（3分）

第三个路口　　 红灯　　 绿灯　 红灯　 绿灯　 红灯　　绿灯　 红灯　　绿灯-（6分）

至少遇到一次红灯的概率为；不遇到红灯的概率为　（10分）

23．简证：∵AB=BC，PB⊥AC

∴AP=CP -------------------------------4分

∴∠MPB=∠CPB----------------------7分

∵PB⊥BC且BC为半圆的直径，

∴PB为半圆的切线------------------10分

又∵PN为半圆的切线

∴∠BPC=∠CPN---------------------13分

∴∠MPB=∠BPC=∠CPN-----------14分

24、（1）可行，------------------------------------1分

由SAS得△ABC≌△DEC-----------------3分

（2）可行，-------------------------------------4分

由AAS得△ABC≌△EDC------------------6分

（3）可得∠B=∠CDE=90°，------------------------------7分

成立，-------------------------------------------------------8分

由AAS得△ABC≌△EDC ----------------------------------9分

（4）能；---------------------------------------------------10分

由△ABC∽△EDC得，--------------------12分

∴AB=n·DE=mn------------------------------------14分