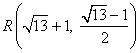第Ⅰ卷（选择题，共10小题30分）
一、选择题（每小题3分，共30分）
1．一元二次方程
的解是（ ）
A．
B．
C．
D．
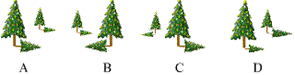
2．下列四幅图形中，表示两颗圣诞树在同一时刻阳光下的影子的图形可能是（ ）
3．“圆柱与球的组合体”如左图所示，则它的三视图是（ ）
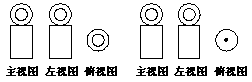
A． B．
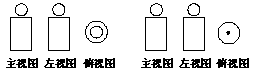
C． D．
4．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例，如下图表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数解析式为（ ）
A．
B．
C．
D．
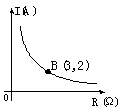
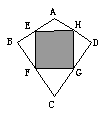
（第4题图） （第6题图）
5．用配方法解一元二次方程
，则方程可变形为（ ）
A．
B．
C．
D．
6．某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝，点E、F、G、H分别是四边形ABCD各边的中点。其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均不计余料）。若生产这批风筝需要甲布料30匹，那么需要乙布料（ ）匹
A．15 B．20 C．30 D．60
7．下列四个命题中错误的是（ ）
A．两条对角线互相垂直且相等的四边形是正方形
B．菱形的一条对角线平分一组对角
C．顺次连结四边形的各边中点所得的四边形是平行四边形
D．等腰梯形的两条对角线相等
8． 如图，点D、E、F分别是△ABC（AB＞AC）各边的中点，下列说法中，错误的是（ ）
A．EF与AD互相平分
B．
C．AD平分∠BAC
D．△DEF∽△ACB
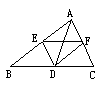
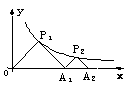
（第8题图） （第10题图）
9．已知反比例函数
的图象上有两点A（
，
），B（
，
），且
，则
的值是（ ）
A．正数 B．负数
C．非正数 D．不能确定
10．如图，△P1OA1、△P2A1A2是等腰直角三角形，点P1、P2在函数
的图象上，斜边OA1、A1A2都在
轴上，则点A2的坐标是（ ）
A．（
，0） B．（
，0）
C．（
，0） D．（
，0）
第Ⅱ卷（非选择题，共14小题90分）
二、填空题（共6题，每小题3分，共18分）
11．近视眼镜的度数y（度）与焦距x（米）的函数关系式为
，已知某同学近视眼镜镜片的焦距为0. 25米，则该同学配的镜片的度数是__________度.
12．将分别标有数字1，4，8的三张卡片洗匀后，背面朝上放在桌面上。随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成两位数恰好是“18”的概率为_________.
13．如图，四边形ABCD是正方形，E是AB延长线上一点，且BE = DB，则∠DFB =_______.
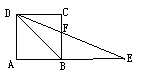
（第13题图） （第15题图）
14．从鱼塘打捞草鱼240尾，从中任选9尾，称得每尾的质量分别是1. 5，1. 6，1. 4，1. 6，1. 2，1. 7，1. 8，1. 3，1. 4（单位：kg），依此估计这240尾草鱼的总质量大约是_______kg.
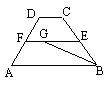
15．如图，已知EF是梯形ABCD的中位线，若AB = 8，BC = 6，CD = 2，∠B的平分线交EF于G，则FG的长是_____________.
16．若函数的图象经过点（2，1），则函数的表达式可能是________________（写出一个即可）.
三、解答题（共8题，72分）
17．（本题6分）解方程：
18．（本题7分）如图，四边形ABCD是菱形，CE⊥AB，交AB的延长线于E，CF⊥AD，交AD的延长线于F。请你猜猜CE与CF的大小有什么关系？并证明你的猜想.
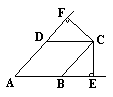
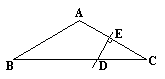
19．（本题7分）如图，在△ABC中，AB = AC，∠B = 30°，AC的垂直平分线DE交BC于D，交AC于E，试说明BD = 2DC.
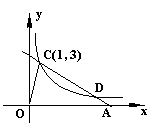
20．（本题8分）如图，反比例函数图象在第一象限的分支上有一点C（1，3），过点C的直线y = kx + b〔k < 0〕与x轴交于点A.
（1）求反比例函数的解析式；
（2）当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时，求△COA的面积.
21．（本题10分）有一块长为32 m、宽为20 m的矩形鲜花试验基地，准备修筑同样宽的三条直路（如图）把基地分成大小相等的六块作为试验田，种植不同品种的郁金香。要使试验田面积为504 m2，求道路的宽。
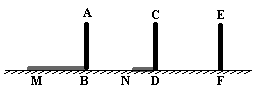
22．（本题12分）电线杆上有一盏路灯O，电线杆与三个等高的标杆整齐划一地排列在马路的一侧，AB、CD、EF是三个标杆，相邻的两个标杆之间的距离都是2 m，已知AB、CD在灯光下的影长分别为BM = 1. 6 m，DN = 0. 6m.
（1）请画出路灯O的位置和标杆EF在路灯灯光下的影子。
（2）求标杆EF的影长。
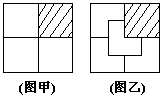
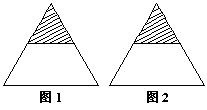
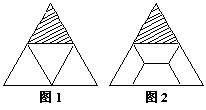
23．（本题10分）如图，把一个正方形割去四分之一，将如下的部分分成3个相同的部分（图甲）；将如下的部分分成4个相同的部分（图乙）。仿照示例，请你将一个正三角形割去四分之一后余下的部分，
（1）分成3个相同的部分（在图1中画出示意图）；
（2）分成4个相同的部分（在图2中画出示意图）。你还能利用所得的4个相同的部分拼成一个平行四边形吗？若能，画出大致的示意图。
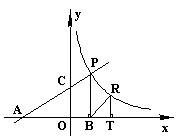
24．（本题12分）如图，直线
分别交轴、
轴于点A、C，已知P是该直线在第一象限内的一点，PB⊥轴于点B，
。
（1）求△AOC的面积；
（2）求点P的坐标；
（3）设点R与点P在同一反比例函数的图象上，且点R在直线PB的右侧，作RT⊥轴于点T，是否存在点R使得△BRT与△AOC相似，若存在，求点R的坐标；若不存在，说明理由。
2005—2006学年度上学期末Ⅰ
参 考 答 案
一、选择题
A、A、C 、A、B、C、A、C、D、C.
10．提示：P1（2，2），OA1=4，设A1A2
= m，则P2（4 +
m，m），代入
即可。
二、填空题
11．400
12．
13．112. 5° 14．360
15．2
16．如：
等
三、解答题
17．
18．提示：连AC，AC平分∠DAB。
19．提示：连AD，证CD = AD =BD。
20．（1）
；
（2）D（3，1），
直线CD：
，A（4，0），
△COA的面积为6.
21．设道路的宽为x，则六个小试验田的长与宽分别为
和
，得
解得：
，
（舍去）
答：道路的宽为2米。
22．（1）如图；
（2）设EF的影长为FP =x，可证：
，得：
，
解得：
。所以EF的影长为0. 4 m.
23．
24．（1）A（－4，0），C（0，2），
△AOC的面积为4；
（2）P（2，3）
（3）由P（2，3）得反比例函数为
。
当△RBT∽△ACO时，
，设BT = m，则RT = 2m，
R（2 + m，2m），代入得，
m1=－3（舍），m2 =1，R（3，2）
当△RBT∽△CAO时，
同理得：BT = 2RT，设RT = n，BT = 2n，
得：R（2 + 2n，n），代入得：
（舍去负值），
