上虞市2005年初三数学竞赛试卷
（2005年12月24日8：30——10：30）
| 题 次 | 一 | 二 | 三 | 总 分 | |||
| 13 | 14 | 15 | 16 | ||||
| 得 分 | |||||||
| 阅卷人 | |||||||
一、选择题：（本题有6小题，每小题5分，共30分）
1、已知
，
，
，则
的值为( )
A、2 B、3 C、4 D、5
2、如图是一个立方体的表面展开图，已知立方体的每一个面上都有一个实数，且相对面上的两数互为倒数，那么代数式
的值等于（
）
A、
B、
C、
D、
3、对于
的方程
，如果方程的实数根个数恰好为3个，则
的值等于（
）
A、1 B、
C、2 D、
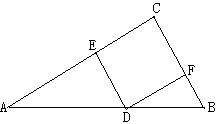
4、如图，把正△ABC的外接圆对折，使点A落在弧BC的中点F上，若BC=5，则折痕在△ABC内的部分DE长为（ ）
A、
B、
C、
D、
5、将一正方形分割成
个（＞1）小正方形，则在下列数据中，不可能取的数是（
）
A、4 B、5 C、8 D、9
6、已知点P（37，27），过P点的直线交X轴、Y轴的正半轴于A、B，则△ABO面积的最小值是（ ）
A、2003 B、2002 C、2000 D、1998
二、填空题：（本题有6小题，每小题5分，共30分）
7、已知不等式
≥0的正整数解为1，2，3，则
的取值范围是
．
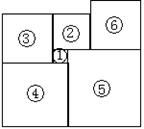8、在一次剪纸活动中，小聪依次剪出6张正方形纸片拼成如图所示的图形，若小聪所拼得的图形中正方形①的面积为1，且正方形⑥与正方形③面积相等，那么正方形⑤的面积为
．
9、如图，R
△ADE、R△BDF和正方形EDFC组成一个大直角三角形ABC，若AD=12
，BD=10，那么图中阴影部分的面积是
．
10、若
，
，并且有正整数满足
，则
．
11、已知梯形ABCD内接于⊙O，AB∥CD，⊙O的半径为4，AB=6，CD=2，则梯形ABCD的面积为 ．
12、已知、
是实数且满足
，设M=
，则M的取值范围是
．
三、解答题：（本题有4小题，每小题15分，共60分）
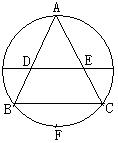
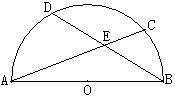
13、如图，设AB为半圆直径，弦AC和BD交于点E，求证：AB
．
14、某市出租车的起步费定为5元（可行驶2千米），往后每多行1千米的车费增加2元（不足1千米按1千米计算），某星期天小聪同学从甲地到乙地乘出租车共付车费35元；如果从甲地到乙地先步行800米，然后乘出租车也需付车费35元。求小聪从甲乙两地中点乘出租车到乙地需支付多少车费？
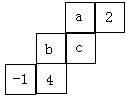
15、如图，正方形EFGH内接于△ABC，设BC=
（表示一个两位数），EF=
，
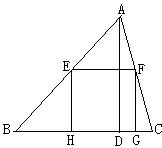三角形中高线AD=
，已知，
，，恰好是从小到大的四个连续正整数，试求△ABC的面积．
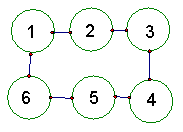
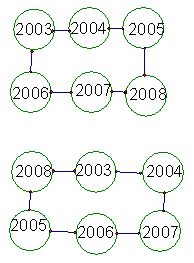
16、图中各个圆圈内分别填上2003，2004，2005，2006，2007，2008六个数，采取如下步骤：将用线段连结的任意相邻的一对数减去同样的数（各次所减的数不必相等）．问：
（1）能否从图一得到图二，若能，写出变化过程；若不能，请说明理由．
（2）能否从图一得到图三，请写出你的的推理过程．
上虞市2005年初三数学竞赛试卷
参考答案及评分意见
一、选择题：
1、B 2、A 3、C 4、B 5、B 6、D
二、填空题：
7、
＜ 8、36 9、60 10、
11、
或
12、
三、解答题
13、证明：正确作出三条辅助线得3分；正确写出两对相似三角形得4分；正确写出两组比例线段得4分；相加并得出结果得4分．
14、解：设从甲地到乙地的总路程为千米，则
及 
，（5分）化简得：
［］＝16 及
得16＜≤17 及16＜
≤17
即16.8＜≤17，（5分） 那么
＜
≤
所以小聪从甲乙两地中点乘出租车到乙地需支付车费5+7×2=19元．（5分）
15、分析：由题意可知：a、b、c、d为连续四个整数故可设为a，a＋1，a＋2，a＋3，其中BC＝11a＋1，（1≤a≤8的正整数）（5分）由题意△AEF∽△ABC可得：
解得a＝1；a＝5（5分）可求得△ABC的面积为24或224．均符合题意（5分）．
16、解：（1）能（2分）．变化过程如下：（正确得5分）
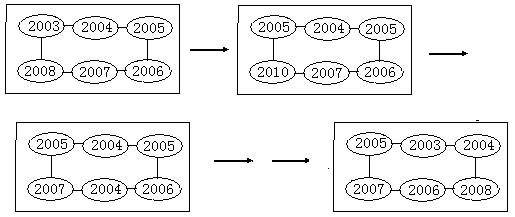
（2）不能（2分）．
因为每一步都改变（如图）：
，是一个定值．（3分）
而图一中S1=（2008+2004+2006）-（2003+2007+2005）=3，（1分）
而图三中S3=（2005+2003+2007）-（2008+2006+2004）=-3 （1分）
显然S1≠S3，故不能从图一得到图三（1分）．
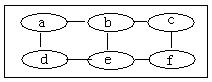
16、 第二题：（本解法供大家讨论）
把各数定为1、2、3、4、5、6如上图的六个位置，则可知1位增大5；2位增大－1；3位增大－1；4位增大1；5位增大－1；6位增大－3；而1位上的变化同2,6两位相连，所以1位上的增大5可以看作1位增大x，6位增大5－x得到，依次可得5位增大－1是由4位上增大1－x和6位上增大－2＋x得到。而（5－x）＋（－2＋x）＝3≠－3矛盾，所以从图1是得不到图3。
