上虞市2005学年度第一学期九年级学业评估考试
数学卷
亲爱的同学,貌似困难的数学最怕有信心的你，严谨的数学需要踏实仔细的你．考试中请注意：
1．全卷共三大题，满分150分.考试时间120分钟.请直接在试卷相应的位置上书写答案.
2.考试中可以使用计算器．
| 题 次 | 一 （1—12） | 二 （13—18） | 三 | 总 分 | ||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得 分 | ||||||||||
| 阅卷人 | ||||||||||
一、精心选一选（本题有12小题，每小题4分，共48分）
1．当X=-3时，下列分式：①
；②
；③
；④
，其中有意义的是（ ）
A、只有① B、只有④ C、只有①③ D、只有②④
2．如图1，D、E、F分别为△ABC三边中点，则与△DEF全等的三角形共有（ ）
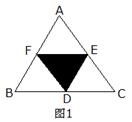（A）1个 （B）2个 （C）3个 （D）5个
3．方程
的根是（ ）
(A) 0 (B)1 (C) 1和-1 (D) 0和1
4．若分式
中的x、y的值都变为原来的3倍，则此分式的值（ ）
（A）不变 （B）是原来的3倍 （C）是原来的
（D）是原来的
5．关于x的一元二次方程
的一个解是0，则a的值是（ ）
A． 1 Ｂ． -1 Ｃ． 1或-1 Ｄ． 
6．已知⊙O1和⊙O2的半径分别为5和2，O1O2＝3，则⊙O1和⊙O2的位置关系是（ ）
（A）外离 （B）内切 （C）相交 （D）外切
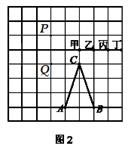
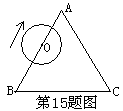
7．如图2，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△ABC ≌△PQR，则点R应是甲、乙、丙、丁四点中的（ ）
（A）甲 （B）乙 （C）丙 （D）丁
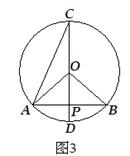
8．如图3，在⊙O中，P是弦AB的中点，CD是过点P的直径，则下列结论中不正确的是（ ）
(A)AB⊥CD (B)∠AOB =4∠ACD
(C)AD与BD这两条弧相等 (D)PO =PD
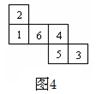
9.一个均匀的立方体六个面上分别标有数1，2，3，4，5，6．图4是这个立方体表面的展开图．抛掷这个立方体，则朝上一面上的数恰好等于朝下一面上的数的
的概率是（ ）
（A）
（B）
（C）
（D）
10．下列命题为假命题的是（ ）
Ａ．同位角相等
Ｂ．菱形的两条对角线相互垂直
Ｃ．对顶角相等 Ｄ．全等三角形的对应边相等
11．根据下列条件，能唯一画出△ABC的是（ ）
（A）AB =3，BC =4，AC =8 （B）AB =4，BC =3，∠A =30º
（C）∠C =90º，AB =6 （D）∠A =60º,∠B =45º，AB =6
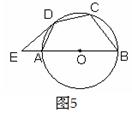
12．如图5，四边形ABCD的四个顶点恰好在⊙O上，且AB是⊙O的直径，过点D的切线交BA的延长线于点E，若∠ADE =28°，则∠C的度数为（ ）
（A）1160 （B）1180 （C）1200 （D）1220
二．细心填一填（本题有6小题，每小题5分，共30分）
13．学汽车驾驶首先要通过交通法规等内容的理论考试．按规定达到90分及以上为通过.小芳在理论考前进行了5次模拟测试，成绩分别为86分，90分，93分，89分，94分，则她在正式考试中能通过的可能性为 .
14. 已知圆锥的底面直径为4，母线为6，则它的侧面积为 ．
15.如图⊙0的半径为1，圆心O，在正三角形的边AB上沿图中的方向移动，当⊙0移动到与AC边相切时，OA的长为 ．
16．请给出一元二次方程
＝0的一个整数常数项，使这个方程有两个不相等的实数根．
17．湖北省某地前段时间发生了禽流感，为补偿该地禽类养殖户的损失，当地政府决定给予养殖户每斤3元的补助，养鸡专业户王大伯养了2000只鸡，工商部门随机抽取了10只鸡，称得重量统计如下表：
| 重量（单位：kg） | 2 | 2.2 | 2.5 | 2.8 | 3 |
| 数量（单位：只） | 1 | 2 | 4 | 2 | 1 |
王大伯可以得到___________元的补偿款．
18．据2005年10月8日《绍兴日报》报道：今年“十一”黄金周期间，我市实现旅游收入再创历史新高，旅游消费呈现多样化，其中住宿消费为3438.24万元，占整个旅游消费的22.62％．
（1）该市今年“十一”黄金周期间的旅游消费共 亿元．
（2）对于“十一”黄金期间的旅游消费，如果我市2007年要达到3.42亿元的目标，那么，2005年到2007年的平均增长率为 ％．
三．耐心解一解(本大题有7个小题，共72分)
温馨提示：亲爱的同学,以下各题都要写出具体的解答过程.
19. (本题12分) 计算:（1）
.
（2）
．
20. (本题12分) 解方程：（1）
．
（2）
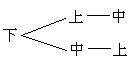
21．(本题8分)在“全民读书月”活动中，小华在书城买了一套科普读物，有上、中、下三册，要整齐的摆放在书架上，有哪几种摆法？请你用树状图进行分析，并求出其中恰好摆成“上、中、下”顺序的概率是多少．
解：
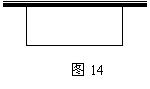
22．(本题9分)课外植物小组准备利用学校仓库旁的一块空地，开辟一个面积为130平方米的花圃（如图14），打算一面利用长为15米的仓库墙面，三面利用长为33米的旧围栏，求花圃的长和宽．
解：
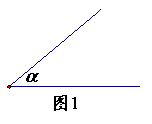23.（本题9分）尺规作图并解答：
如图1，已知
．（作图要求保留作图痕迹）
（1） 求作：
，使
；
（2） 求作：的平分线
；
（3） 
是的平分线上任意一点，作出以为圆心并与
相切于
点的⊙O．说明⊙O与
相切．
24.(本题有3小题，第(1)小题为必答题，满分5分；第(2)、(3)小题为选答题，其中，第(2)小题满分3分，第(3)小题满分5分，请从中任选1小题作答，如两题都答，以第(2)小题评分.)
在△ABC中，∠ACB =90°，AC =BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
(1)当直线MN绕点C旋转到图10-1的位置时，求证：
①△ADC ≌△CEB ；
②DE =AD +BE.
(2)当直线MN绕点C旋转到图10-2的位置时，求证：DE =AD -BE；
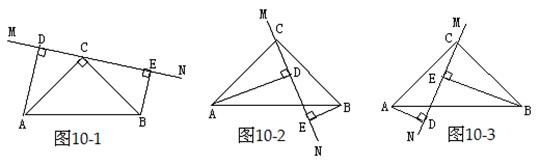(3)当直线MN绕点C旋转到图10-3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.
注意：第(2)、(3)小题中，你选答的是第 小题.
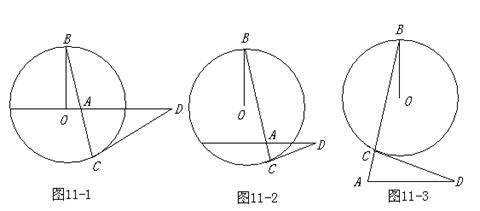
25．(本题1２分)如图11-1,已知点A是⊙O直径上一点，OB是与这条直径（线）垂直的半径，BA与⊙O相交于点C，过点C作切线与OA的延长线相交于点D.
（1）试证明：DA =DC；
（2）将直线DA向下平移到半径OB外，如图11-2，那么DA与DC之间存在什么关系？（此小题只须说明结论，不必证明）
（3）将直线DA平移到⊙O外，如图11-3，那么DA与DC之间又存在什么关系？请你说明理由.
上虞市2005学年度第一学期九年级学业评估考试数学卷
参考答案及评分标准
一．精心选一选：
1．A 2.C 3.D 4.A 5.B 6.B 7.B 8.D 9.A 10.A 11.D 12.B
二.细心填一填:
13.
14.12
15.
16.小于16的任一整数均可以.
17.15000 18.(1)1.52 (2)50
三.耐心解一解:
19. (本题12分)解:（1）原式=
(4分) =
(2分)
（2）解：原式=
…(1+2+1=4分) =
…(1分) =
……(1分)
20. (本题12分)（1）x1=1,x2=3 (6分)
（2）解：去分母得：
……(2分)
去括号得：
解得： 
……(2分)
经检验, 是原方程的解. (1分)
所以原方程的解为.……(1分)
21. (本题8分)解:作出树状图如下：
，
，
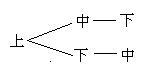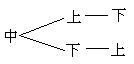……（3分）
所以总共有6种摆法。……（2分）
在这6种摆法中，恰好摆成“上、中、下”顺序的只有1种，所以摆成“上、中、下”顺序的概率P=
……（3分）
22. (本题9分)
解：（方法一）设与墙相接的两边长都为
米，则另一边长为
米，（1分）
依题意得：
… （ 2分）
整理得：
∴
（ 3分）
又∵ 当时， 
＜15
但当时，此时
＞15 ∴
不合题意，舍去．（ 1分）
∴
此时， （ 1分）
答：花圃的长为13米，宽为10米． …… （ 1分）
（方法二）设与墙平行的一边长为米，则与墙相接的两边长都为
米，…… （ 1分）
依题意得：
…… （ 2分）
整理得：
∴
， 
…… （ 3分）
又∵ ＞15 （1分）
∴不合题意，舍去． ∴
，=10 …… （1分）
答：花圃的长为13米，宽为10米． …… （ 1分）
23．（本题９分）作图并解答：
解：（1）、（2）、（3）作图如下：……（2+2+1=5分，注意：非尺规作图不给分，注意看图1中是否有圆弧）
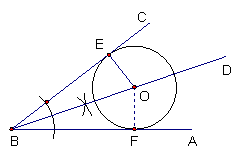
（3）证明：过O作OF⊥BA，…… （ 1分）
∵⊙O与相切于点，E为切点（已知）
∴OE是⊙O的半径且OE⊥BC（圆的切线的定义）…… （ 1分）
又∵是的平分线上任意一点，且OF⊥BA（已知）
∴OE=OF（角平分线的意义）…… （ 1分）
即OF是⊙O的半径， ∴⊙O与相切（圆的切线的定义）……
（ 1分）
24.(1)证明:①∵∠ACB=900, ∴∠ACD+∠BCE=900,
∵AD⊥MN于点D, ∴∠DAC+∠ACD=900,∴∠DAC=∠BCE,
而AC=BC, ∠ADC=∠CEB=900, ∴△ADC≌△CEB (AAS) (3分)
②由△ADC≌△CEB，∴AD=CE,DC=BE, ∴DE= CE+DC=AD+BE. (２分)
(2)只须证明△ACD≌△CBE,CD=BE,AD=CE,则DE=EC-DC=AD-BE. (3分)
(3)等量关系为：DE=BE-AD. (2分)
证明如下:
∵∠ACB=900, ∴∠ACD+∠BCE=900,
∵BE⊥MN于点E, ∴∠EBC+∠BCE=900, ∴∠EBC=∠DCA,
而∠BEC=∠CDA=900,AC=BC, ∴△ACD≌△CBE (AAS) (2分)
∴BE=CD,AD=CE, ∴DE=CD-CE=BE-AD. (1分)
25. (本题12分) (1)证明:连结OC, ∵DC切⊙O于点C, ∴∠DCO=900, ∴∠DCA=900-∠OCA,
∵OB=OC,∴∠B=∠OCA, ∴∠DCA=900-∠B,
又∵BO⊥OD,∴∠BAO=900-∠B, 而∠BAO=∠DAC,∴∠DAC=∠DCA, ∴DA=DC. （４分）
(2)仍有结论:DA=DC (2分)
(3)存在关系: DA=DC. (２分)
这是因为:连结OC,延长BO交AD于E,
∵BO⊥AD,∴∠A=900-∠B, ∵DC切⊙O于点C,∴∠OCD=900,
而B、C、A三点共线，∴∠BCA=1800，∴∠DCA=900-∠OCB，
又∵OB=OC，∴∠B=∠OCB，∴∠A=∠DCA，∴DA=DC. (４分)