九年级数学（上）学习达标检测
（时间：90分钟 满分：100分）
班级 学号 姓名 得分
一、选择题（每题4分，共32分）
1、已知扇形的圆心角为120°，弧长等于半径为5㎝的圆周长，则扇形的面积为（ ）
A、75㎝2 B、75π㎝2 C、150㎝2 D、150π㎝2
2、半径相等的圆内接正三角形、正方形、正六边形的边长之比为（ ）
A、1：2：3 B、
C、
D、3：2：1
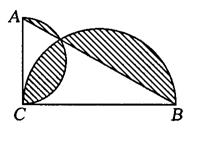3、如图，直角三角形ABC中，∠C=90°，AC=2，AB=4，分别以
AC、BC为直径作半圆，则图中阴影的面积为 （ ）
A、
B、
C、
D、
4、一个扇形的半径为30㎝，圆心角为120°，用它做成一个圆锥
的侧面，则圆锥的底面的半径是 （ ）
A、10㎝ B、12㎝ C、14㎝ D、15㎝
5、若圆锥的底面直径为6㎝，母线长为5㎝，那么圆锥的侧面积为 （ ）
A、7.5π㎝2 B、30π㎝2 C、15π㎝2 D、22.5π㎝2
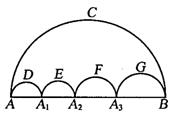6、如图，图中有五个半圆，邻近的两个半圆相切，两只小虫同时
出发，以相同的速度沿弧ADA1、弧A1EA2、弧A2FA3、弧A3GB路线爬
行，乙虫沿弧ACB路线爬行，则下列结论正确的是 （ ）
A、 甲先到B点
B、 乙先到B点
C、 甲、乙同时到B点
D、 无法确定
7、在Rt△ABC中，已知AB=6，AC=8，∠A=90°，如果把此直角三角形绕直线AC旋转一周得到一个圆锥，其表面积为S1；把此直角三角形绕直线AB旋转一周得到另一个圆锥，其表面积为S2，那么S1：S2等于
（ ）
A、2：3 B、3：4 C、4：9 D、5：12
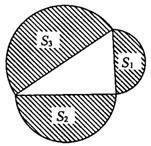
8、如图，直角三角形三边上的半圆面积从小到大依次记为S1、
S2、S3，则它们之间的关系正确的是 （ ）
A、S1+S2>S3 B、S1+S2<S3 C、S1+S2=S3 D、S12+S22=S32
二、填空题（每题4分，共24分）
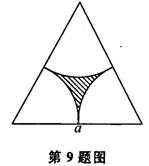
9、如图所示，边长为a的正三角形中阴影部分的面积为 。
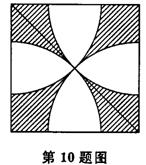
10、如图，在边长为1的正方形中，以各顶点为圆心，对角线长的一半为半径在正方形内画弧，则图中阴影部分的面积为 。
11、圆锥的底面半径为2㎝，高为
㎝，
则这个圆锥表面积 。
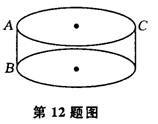
12、如图，一圆柱体积的底面周长为24㎝，高AB
为4㎝，AC是直径，一只蚂蚁从点A出发沿着圆柱
体的表面爬行到C的最短路程大约是 。
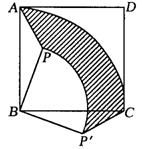13、已知，点P是正方形ABCD内的一点，连结PA、PB
将△PAB绕点B顺时针旋转90°到△
CB的位置。设
AB的长为a，PB的长为b（b<a），则△PAB旋转到△PCB的
过程中点P转过的路径长度 ，边PA所扫过区域
（图中阴影部分）的面积 。
14、现用总长为80米的建筑材料，围成一个扇形花坛，
当扇形半径为 时，可使花坛的面积最大。 (第13题图)
三、解答题（15、16题每题6分，17-20题每题8分，共44分）
15、如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D，已知AB=24㎝，CD=8㎝。
（1）作此残片所在的圆（不写过程，保留作图痕迹）。
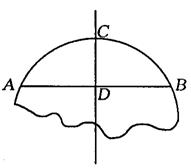（2）求（1）中所作圆的半径。
16、圆锥的底面半径为3㎝，侧面展开图是圆心角为120°的扇形，求圆锥的全面积。
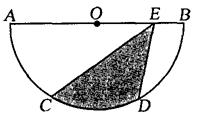
17、如图，AB为半圆O的直径，C、D是⊙O上的三等分点，若⊙O的半径为1，E为线段AB上任意一点，计算图中阴影部分的面积。
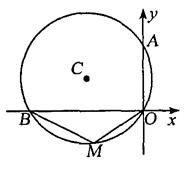
18、如图，⊙C经过原点且与两坐标轴分别交于点A与点B，点A的坐标为（0，4），M是圆上一点，∠BMO=120°。求：⊙C的半径和圆心C的坐标。
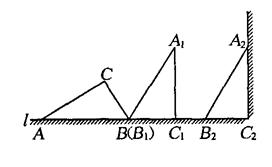
19、如图，在一个横截面为Rt△ABC的物体中，∠ACB=90°，∠CAB=30°，BC=1米。工人师傅把此物体搬到墙边，先将AB边放在地面（直线l）上，再按顺时针方向绕点B翻转到△A1B1C1的位置（BC1在l上），最后沿BC1的方向平移到△A2B2C2的位置，其平移的距离为线段AC的长度（此时A2C2恰好先靠在墙边）
（1）直接写出AB、AC的长度；
（2）画出在搬动此物的整个过程A点所经过的路径，并求出该路径的长度（精确到0.1）
20、学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下讨论：
甲同学：这种多边形不一定是正多边形，如圆内接矩形；
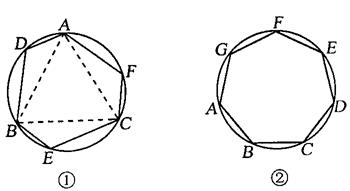
乙同学：我们发现边数是6时，它也不一定是正多边形。如图①，△ABC是正三角形，AD=BE=CF可以证明六边形ADBECF的内角相等，但它未必是正六边形；
丙同学：我能证明，边数是5时，它是正多边形。我想，边数是7时，它可能也是正多边形……
（1） 请你说明乙同学构造的六边形各内角相等；
（2） 请你证明，各内角都相等的圆内接七边形ABCDEFG，如图②是正七边形（不必写已知，求证）；
（3） 根据以上探索过程，提出你的猜想（不必证明）
九年级数学（上）.学习达标检测答案
一、1、B 2、C 3、D 4、A 5、C 6、C 7、B 8、C
二、9、
10、
11、6π㎝2 12、
㎝ 13、（1）
（2）
14、20㎝
三、15、（1）略 （2）13㎝ 16、36π㎝2 17、
18、⊙C的半径为4，C（
，2）
19、（1）AB=2米 AC=
米 （2）约5.9米
20、略。