九年级数学第二次月考试卷
班级______ 座号____ 姓名________ 成绩
一、填空题（每题3分，共45分）
1.反比例函数y=-3/2x的图象的两个分支分别在第_________象限内。
2.如果
与
成反比例，z与成正比例，则z与成____
______；
3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜的镜片的焦距为0.25m，那么眼镜的度数y与镜片焦距x之间的函数关系式为______________。
4.若A（-2，a-4）在反比例函数y=
的图象上，那么a=_____.
5.教室中的矩形窗框在太阳光的照射下，在地面上的影子是 .
6.老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：
甲：函数的图象经过第一象限 乙：函数的图象经过第三象限；
丙：在每个象限内，y随x的增大而减小．
请你根据他们的叙述构造满足上述性质的一个函数：_______________。
7.当三角形的面积为12cm2时，它的底边acm与这个底边上的高hcm的函数关系式是_________。
8.已知y与（2x+1）成反比例，且当x=1时，y=2，那么当x=2时，y=____________。
9．李栓身高
，王鹏身高
，他们在同一时刻站在阳光下，李栓的影子长为
，王鹏的影长是 m。
10、小芳的房间有一面积为3m2的玻璃窗，她站在室内离窗子4m的地方向外看，她能看到窗前面一楼房的面积有 m2(楼层之间的位20m).
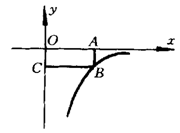11、如图，面积为3的矩形OABC的一个顶点B在反比例函数
则该涵数关系式是_________。
12、点 A（
，
）、B(a-1, 
)均在反比例函数的图y=1/x的
象上，若 ＜0，则 _____；
13．一个四棱锥的俯视图是 ；
14、直角坐标平面内，一点光源位于A(0，5)处，线段CD⊥x轴， D为垂足，C(3，1)，则CD在x轴上的影长为 ，点C的影子的坐标为 .
15、直角坐标平面内，身高1.5米的小强站在x轴上的点A(–10 、0)处，他的前
方5米有一堵墙，若墙高2米，则站立的小强观察y轴时，盲区范围是 .
二、 选择题 （每题4分，共36分）
1.已知四个函数：①y=－x ②y=x+1 ③y=1/x ④y=-1/2x，其中y随x增大而增大的函数有（ ）A. 1个 B. 2个 C. 3个 D. 4个
2. 对于函数y=-1/x，当x<0时，y的取值及对应的这部分图象是（ ）
A. y<0，图象在第二、四象限 B. y<0，图象在第三象限
C. y>0，图象在第一象限 D. y>0，图象在第二象限
3.当路程s一定时，速度v与时间t之间的关系是( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
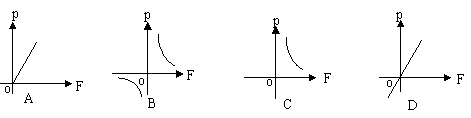4. 受力面积S（m2），（S为常数且m≠0）的物体，所受压强P（pa）与压力F（N）的函数关系为P=
，则这个函数图象为（
）
5．若函数y=k/x的图象过点（3，-7），那么它一定还经过点（ ）
（A）（3，7） （B）（-3，-7） （C）（-3，7） （D）（2，-7）
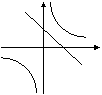
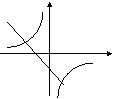
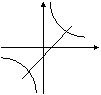6. 在同一坐标系中，函数
和y=kx+3的图像大致是（ ）
 |
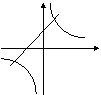A B C D
7. 点（－1，y1），（－2，y2），（
是y=1/3x图象上三个点，则y1，y2，y2 的关系为（ ）A、y2<y3<y1 B、y2<
y1 <y3
C、y1<y2<y3 D、y3<y2<y1
8．如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（ ）
 |  | ||
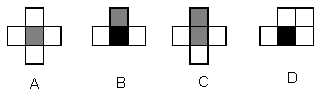9．如图，A、C是函数y=1/x的图象上的任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记RtΔAOB的面积为S1，RtΔCOD的面积为S2则（ ）
A、S1 ＞S2 B． S1 <S2
C、 S1=S2 D． S1与S2的大小关系不能确定
三、解答题：（每题8分，共48分）
1. 在某一电路中，保持电压不变，电流I(安培)与电阻R(欧姆)成反比例，当电阻R=5欧姆时，电流I=2安培。
（1）求I与R之间的函数关系式,并画出函数图象。
（2）当电流I=0.5安培时，求电阻R的值；
2.已知y=y1+y2，y1与(x+1)成正比例，y2与x成反比例，且当x=1时，y=6；当x=－1时，y=－2，求y与x的函数式。
3、(1)一个透明的玻璃正方体内镶嵌了一条铁丝(如图所示的粗线)，请指出右边的两个图是从正方体的哪个方向看到的视图.
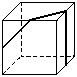
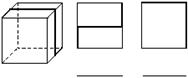(2)如图，粗线表示嵌在玻璃正方体内的一根铁丝，请画出该正方体的主视图、左视图和俯视图.
4．已知□ABCD中，AB = 4，AD = 2，E是AB边上的一动点，设AE=，DE延长线交CB的延长线于F，设CF =，求与之间的函数关系。
5．已知：反比例函数y=k/x和一次函数y=-2x+1其中一次函数的图像经过点（
，5）.
（1） 试求反比例函数的解析式；
（2） 若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标；
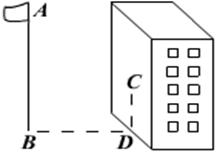
6、如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的应高为2米，求旗杆的高度.
四、解答题
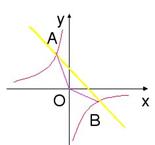
1、已知一次函数y=-x+6和反比例函数y=k/x（
≠0）
（1）满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点（6分）
（2）设（1）中的两个公共点为A，B，则∠AOB是锐角还是钝角（4分）。
2．如图，已知一次函数y=kx+b（≠0）的图象与反比例函数y=-8/x的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是
；
（1） 
一次函数的解析式（5分）。
（2） △AOB的面积（6分）。
五、附加题
1.为了预防春季感冒，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中含药量y(mg)与时间x(min)成正比例；药物燃烧后，y与x成反比例（如图），现测得药物10min燃烧完毕，此时室内空气中每立方米的含药量为8mg，
请根据题中所提供的信息，解答下列问题。
（1）药物燃烧时，y与x的函数关系式为________，自变量x的取值范围为________，药物燃烧后y关于x的函数关系式为___________。
（2）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进入教室，那么从消毒开始，至少需要经过________min后，学生才能回到教室。
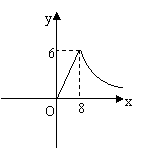（3）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
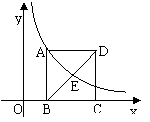2、已知如图，点A（1，3）在函数y=k/x（x>0）的图像上，矩形ABCD的边BC在x轴上，E为对角线BD的中点，函数y=k/x（x>0）的图像又经过A，E两点，点E的横坐标为m。
（1）求k的值。
（2）求点C的坐标（用m的代数式表示）。
（3）当∠ABD=45°时，求m的值。