三洋中学九年级数学阶段测试(月考) 2006.10![]()
(满分150分;完卷时间120分钟)
班级 姓名 成绩
一.选择题(每题4分,共40分)
1. 下列各式中,y是![]() 的二次函数的是( )
的二次函数的是( )
A.
![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
2、反比例函数![]() 的图象在 ( )
的图象在 ( )
(A)第一、三象限 (B)第二、四象限 (C)第一、二象限 (D)第三、四象限
3、已知抛物线的解析式为y=(x-2)2+1,则抛物线的顶点坐标是( )
A、(-2,1) B、(2,1) C、(2,-1) D、(1,2)
4、抛物线![]() 向右平移1个单位,再向上平移2个单位,得到新的图象的二次函数表达式是( )
向右平移1个单位,再向上平移2个单位,得到新的图象的二次函数表达式是( )
A ![]() B
B ![]()
C ![]()
| |
5、抛物线![]() 则图象与
则图象与![]() 轴交点为( )
轴交点为( )
 A. 二个交点 B. 一个交点 C. 无交点 D. 不能确定
A. 二个交点 B. 一个交点 C. 无交点 D. 不能确定
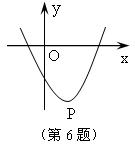
6.如图,抛物线的顶点P的坐标是(1,-3),则此抛物线对应的二次函数有( )
(A)最大值1 (B)最小值-3
(C)最大值-3 (D)最小值1
7、根据下列表格的对应值:
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c=0 | -0.06 | -0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.26
8、已知电压为220伏保持不变 ,则电流 y 与电阻 x 之间的关系用图象大致可表示为
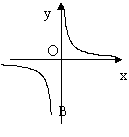
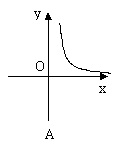
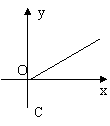
9、已知![]() 是反比例函数
是反比例函数![]() 的图象上三点,且
的图象上三点,且![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
 10、小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数
10、小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数![]() (t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
(A)0.71s (B)0.70s (C)0.63s (D)0.36s
二.填空题:(每题5分,共30分)
11、已知反比例函数y=的图象经过点(1,2),则k的值是_________。
12.
请写出一个开口向上,且对称轴为直线![]() 的二次函数解析式 。
的二次函数解析式 。
13、对于函数![]() ,当
,当![]() 时,y的取值范围是______
时,y的取值范围是______![]() ______;
______;
14.已知抛物线![]() 的顶点在
的顶点在![]() 轴上,则
轴上,则![]() 的值是 。
的值是 。
15、
(见卷)
 16、 两个反比例函数
16、 两个反比例函数![]() ,
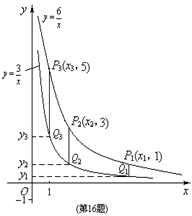
,![]() 在第一象限内的图象如图所示, 点P1,P2,P3,…,P2 005在反比例函数
在第一象限内的图象如图所示, 点P1,P2,P3,…,P2 005在反比例函数![]() 图象上,它们的横坐标分别是x1,x2,x3,…,x2 005,纵坐标分别是1,3,5,…,共2 005个连续奇数,过点P1, P2,P3,…,P2 005分别作y轴的平行线,与
图象上,它们的横坐标分别是x1,x2,x3,…,x2 005,纵坐标分别是1,3,5,…,共2 005个连续奇数,过点P1, P2,P3,…,P2 005分别作y轴的平行线,与![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2 005(x2 005,y2 005),
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2 005(x2 005,y2 005),
则y2 005= .
三.解答题(共80分)
17、(6分)已知![]() 是
是![]() 的反比例函数,当
的反比例函数,当![]() =3时,
=3时,![]() =4,则当
=4,则当![]() =2时求函数
=2时求函数![]() 的值。
的值。
18.(6分)求二次函数y=x2+2x-4图象的开口方向、对称轴、顶点坐标。
19、(8分)若一个面积为20cm2的矩形的宽y(cm),长x(cm)。
(1)直接写出y与x的函数关系式,以及自变量x的取值范围。
(2)在右方格中用描点法画出所求函数的图象。
(2)当长满足5≤x≤10时,求宽y的取值范围。
20.(8分)已知二次函数的图象的顶点坐标为(3,-2)且与![]() 轴交与(0,
轴交与(0,![]() )
)
(1)求这个二次函数的解析式。
(2)若这抛物线经过点![]() ,请你先画出草图,再根据草图试比较
,请你先画出草图,再根据草图试比较![]() 的大小。
的大小。
21、(6分)下面两题,任选一题完成,如果两题都做,则按第(1)题给分。
l
第(1)题、我们学习过反比例函数,例如,当矩形的面积S一定时,长a是宽b的反比例函数,其函数关系式可以写为![]() )S为常数,S≠0).
)S为常数,S≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:_________________________________.
函数关系式:______________________________.
l 第(2)题、老师在同一直角坐标系中画了一个反比例函数的图象以及正比例函数y=-x的图象,请同学们观察有什么特点。同学甲说:与直线y=-x没有交点;同学乙说:图象上任意一点到两坐标轴的距离的积为5。请你根据同学甲和同学乙的说法写出反比例函数的解析式。
解析式为: 。
大致理由为:
。
22、(本题8分)、如图,已知正比例函数![]() 与反比例函数
与反比例函数![]() 的图象都过A(m,1)点。
的图象都过A(m,1)点。
(1)求m的值,并求反比例函数的解析式。(4分)
(2)求正比例函数与反比例函数的另一个交点B的坐标。(4分)
 23、(9分)在直角坐标平面中,O为坐标原点,二次函数
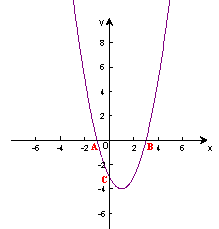
23、(9分)在直角坐标平面中,O为坐标原点,二次函数![]() 的图象与x轴的负半轴相交于点C(如图5),点C的坐标为(0,-3),且BO=CO
的图象与x轴的负半轴相交于点C(如图5),点C的坐标为(0,-3),且BO=CO
(1) 求出B点坐标和这个二次函数的解析式;
(2) 求△ABC的面积。
(3) 设这个二次函数的图象的顶点为M,求AM的长.
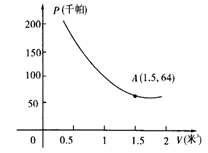
24、(10分)某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
 (1)写出这个函数的解析式;
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
25、(10分)农民张大伯为了致富奔小康,大力发展家庭养殖业,他准备用40米长的木栏围一个矩形的养圈,为了节约材料,同时要使矩形面积最大,他利用了自己家房屋一面长25米的墙,设计了入图一个矩形的养圈。
(1)请你求出张大伯设计的矩形羊圈的面积。
 (2)请你判断他的设计方案是否使矩形羊圈的面积最大?如果不是最大,应怎样设计?请说明理由。
(2)请你判断他的设计方案是否使矩形羊圈的面积最大?如果不是最大,应怎样设计?请说明理由。
 26、(10分)右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
26、(10分)右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
(1)求抛物线的解析式.(6分)
(2)求两盏景观灯之间的水平距离.(4分)