2005—2006年度第一学期期末考试
初三年级数学试题
一、填空题（本大题共10小题，每小题2分，共20分）
1、写出一个图象在二、四象限的反比例函数的解析
式 .
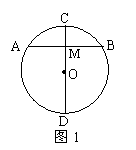
2、如图1，⊙O的直径CD与弦AB交于点M，添加一个条件
得到M是AB的中点.
|
的自变量x的取值范围是 .
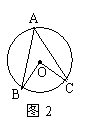
4、如图2，在⊙O中，BC 的度数是100°，点A在⊙O上，
则∠BAC的度数是 .
5、生产一种药品，原来每件成品是100元，由于连续两次降低成
本，现在的成本是81元，则平均每次降低成本的百分率为 .
6、已知⊙O的半径为2，点P到圆心O的距离为
，那么点P在⊙O
（填“外”、“内”、“上”）
7、抛物线y=(x-1)2+2的顶点坐标是 .
8、若一个梯形内接于圆，有如下四个结论：①它是等腰梯形；②它是直角梯形；
③它的对角线互相垂直；④它的对角互补.请写出所有你认为正确结论的序
号 .
9、当m= 时，函数y=(m+3)·x2m+1+4x-5（x≠0）是一次函数.
10、盐中新校区要建一个由若干盆花组成的形如正六边形的花坛，每条边（包括两个
顶点）有n(n>1)盆花，设这个花坛边上花盆的总数为S，请观察下图的规律：
 |
按上规律推断，S与n的关系是 .
二、选择题：（本大题共10小题，11～15题每小题3分，16～20小题每小题4分，计35分）下列各题给出的四个选项中仅有一个是正确的.
11、下列四个函数（1）y=x+1；（2）y=
；（3）y= - x2；（4）y=2x，其中函数的图象是中心对称图形的共有…………………………………………………………[ ]
A、4个 B、3个 C、2个 D、1个
12、下列命题中：（1）三角形有且仅有一个外接圆；（2）垂直于半径的直线是圆的切线；（3）没有公共点的两圆的位置关系一定是外离；（4）正五边形既是轴对称图形又是中心对称图形.其中真命题有…………………………………………………[ ]
A、1个 B、2个 C、3个 D、4个
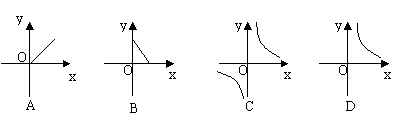13、当矩形的面积是一个常量S（厘米2）时，它的一边长y(厘米)是另一边长x(厘米)的函数，这个函数图象的形状大致是……………………………………………[ ]
14、一个正方形的边心距、外接圆半径与这个正方形边长的比为……………[ ]
A、1:2:
B、1::2 C、1::4 D、:2:4
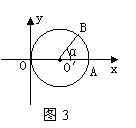15、如图3，点O′的坐标为(1，0),且⊙O′与x轴正半轴交于点A，与射线O′B交于点B，与y轴相切,∠AO′B=∠α（α为常数），则点B的坐标为………………[ ]
A、（cosα，sinα）
B、(1+sinα，cosα)
C、(cosα，1+sinα)
D、(1+cosα，sinα)
16、已知：如图4,⊙O的半径为cm，⊙O′的半径为2cm，⊙O与⊙O′相交于点A、B（点O、O′分别在AB两侧），若AB=2cm，则∠O′AO的度数是………………[ ]
A、105° B、75° C、60° D、45°
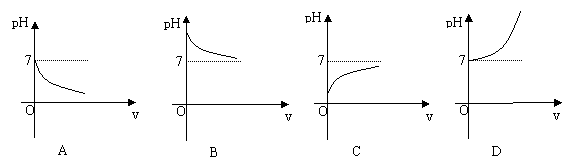17、我们知道，溶液的酸碱度由pH值确定，当pH>7时，溶液呈碱性；当pH<7时，溶液呈酸性。若将给呈酸性的HCl溶液加水稀释，那么下列图象中，能反映HCl溶液的pH与所加水的体积(v)的变化关系是………………………………………[ ]
座位号□□
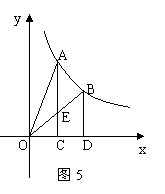
18、如图5，过反比例函数y=
的图像上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连结OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，则比较它们的大小关系是………………………………………………[ ]
A、S1>S2 B、S1=S2 C、S1<S2 D、大小关系不能确定
19、若直线y=x-1与抛物线y=x2+5x+a2相交，则它们的交点必在………………[ ]
A、第一象限 B、第二象限 C、第三象限 D、第四象限
 | |||
 | |||
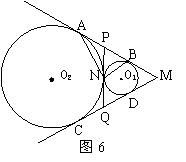20、如图6，半径分别为1cm和3cm的⊙O1与⊙O2外切于N点，AB、CD分别是两圆的外公切线且交于M点，内公切线PQ分别交AB于P，交CD于Q，下列四个结论：①△ABN是直角三角形；②O2、N、O1、M四点共线；③∠AMC=60°；④AB=CD=PQ=2
.其中正确的结论有……………………………………………………………………[ ]
A、4 B、3 C、2 D、1
三、解答题：（本大题共6小题，计35分）
21、（本题满分5分）
计算：sin245°+cos245°-2tan30°·cos30°+cot30°·tan45°
22、（本题满分6分）已知：关于x的方程x2-kx-2=0
（1）求证：方程有两个不相等的实数根；
（2）设方程的两根为x1、x2，如果2（x1+x2）>x1x2，求k的取值范围.
23、（本题满分6分）如图7，在Rt△ABC中，∠C=90°，AC=6，BC=8，
（1）求作⊙O，使得⊙O与AB、AC两边都相切，且圆心O在BC边上
（用尺规作图，不写作法，保留作图痕迹）
（2）求出（1）中⊙O的半径.
24、（本题满分6分）已知：一次函数的图象与双曲线y=-
交于点（-1，m），且过点（0，1）求该一次函数的解析式和直线与双曲线的另一个交点坐标.
25、（本题满分6分）在我市旧城改造中，要将如图8所示的一棵树放倒，在操作过程中，甲要直接将树放倒，乙不同意，他担心这样会损害这棵树周围4.5米处的物体，请你根据图中标注的测量数据，通过计算说明，乙的担心是否有必要（计算中可能用到的数据：≈1.4，
≈1.7，计算结果精确到0.1米）
26、（本题满分6分）
如图9，已知直线MN与以AB的直径的半圆相切于点C，∠A=28°，
（1）求∠ACM的度数；
（2）在MN上是否存在点D，使AB·CD=AC·BC，若存在请作出此点，并予以证明；
若不存在，说明理由.
四、解答题：（本大题共3小题，计25分）
27、（本题满分8分）某单位急需用车，但又不准备买车，他们准备和一个体车主或一国营出租车公司其中的一家签订月租车合同。设汽车每月行驶x千米，应付给个体车主的月费用是y1元，应付给出租车公司的月费用是y2元，y1、y2分别与x之间的函数关系图象（两条射线）如图10，观察图象回答下列问题：
（1）每月行驶的路程在什么范围内，租国营公司的车合算？
（2）每月行驶的路程等于多少时，租两家车的费用相同？费用是多少？
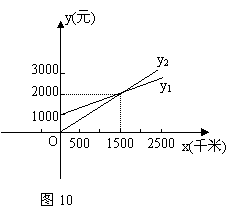（3）如果这个单位估计每月行驶的路程为2300千米，那么这个单位租哪家的车
合算？
28、（本题满分8分）列方程解应用题
某化工厂计划生产300吨化工原料，生产6天后，改进了流程，提高了生产效率，每天比改进前多生产2吨，结果提前4天完成计划，问改进前每天生产原料多少吨？
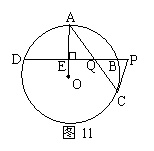29、（本题满分9分）如图11，已知⊙O的两条弦AC、BD相交于点Q，OA⊥BD于E，延长DB至点P，使得PC=PQ
（1）试判断直线PC与⊙O的位置关系，并证明你的结论；
（2）若Q是EB和AC的中点，PB=1，求PQ和AC的长.
五、解下列各题（本大题共3小题，共35分）
30、（本题满分11分）某商场经营一批进价为2元一件的小商品，在市场营销中
发现此商品的日销售单价x元与日销售量y件之间有如下关系：
| x | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
(1)若日销量y件与日销售单价x元之间是一次函数关系，求出y与x之间的函数
关系式.
(2)设经营此商品的日销售利润（不考虑其他因素）为Q元，根据日销售规律，试
求出日销售利润Q元与日销售单价x元之间的函数关系式，并求出日销售单
价x为多少元时，才能获得最大日销售利润。此时最大日销售利润是多少元？
31、(本题满分12分)已知如图12，抛物线y=-x2+bx+c与x轴的两个交点分别为
A（1，0），B（3，0），
(1)求抛物线的解析式；
（2）设点P在该抛物线上滑动，问满足条件S△PAB=1的点P有几个？并求出所有
点P的坐标；
（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的
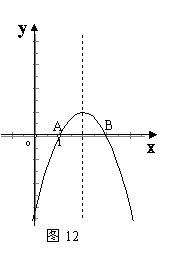周长最小；若存在，求出点M坐标；若不存在，请说明理由.
|
|
B两点，点C为AO2B上一动点（不运动至A、B），连结AC，并延长与⊙O2交于点P，连结BP、BC
|
（2）请猜想△BCP的形状，并证明你的猜想（图13(2)供证明用）
（3）如图13(3)，当PA经过点O2时，AB=4，BP交⊙O1于D，且PB、DB的长是方程x2+kx+10=0的两个根，求⊙O1的半径.
 |