九年级第一学期期末复习
一、选择题（每题3分，共30分）
1、下列方程一定是关于
的一元二次方程的是（ ）
A、
B、
C、
D、
2、顺次连接四边形ABCD各边中点的四边形EFGH，若使四边形EFGH是菱形，应添加的条件为（ ）
A、AD∥BC B、AC=BD C、AC⊥BD D、AD=AB
3、关于x的一元二次方程
有两个相等的实根，则m的取值范围
是（ ）
A、m≥0
B、m>
C、m<
D、m=
4、在□ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（ ）
A、1< m <11 B、2< m <22 C、10< m <12 D、5< m <6
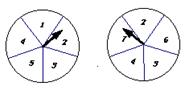
| 5、如图所示的两个圆盘中,指针落在每一个数上的机会均等, 则两个指针同时落在偶数上的概率是（ ） A． |
|
B．
C．
D．
6、在同一地点的灯光下，小明的影子比小强的影子长，则下列说法正确的是（ ）
A、小明比小强高 B、小明比小强矮 C、小明和小强一样高 D、无法判断谁高
7、.三角形两边长分别为3和6，第三边是方程
的解，则这个三角形的周长是（ ）
A、11 B、13 C、11或13 D、11和13
8、若方程
的两根互为相反数，则
的取值为（ ）
A 、5或
B、5 C、 D、以上都不对
9、若反比例函数
的图象在第二、四象限，则
的值是（ ）
A、 －1或1 B、小于
的任意实数 C、 －1 Ｄ、 不能确定
10、某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标志。从而估计该地区有黄羊（ ）
A．200只 B.400只 C .800只 D.1000只
二、填空题（每题3分，共36分）
1. 当
时，方程
是一元二次方程.
2. 一元二次方程
的一个根是-1，则
，另一根是 .
3. 已知y与z成正比例,z与x成反比例,那么
与x成 关系.
4. 一个矩形的投影可能是 .
5. 袋中有3个红球,2个白球,现从中任意摸一球是白球的概率是 .
6. 一块长方形花圃,长为a米,宽为b米,面积为8平方米,那么a与b成的函数关系式为: ,其图象形状是 位置在 象限.
7. 关于x的方程
是一元二次方程，则m的值是
8. 若反比例数
中,y随着x的增大而增大，则k .
9. 用0,1,2能组成三位数的概率是
10. 某钢铁厂今年1月份钢产量为4万吨，三月份钢产量为4.84万吨,每月的增长率相同，问2、3月份平均每月的增长率是
11．电影院呈阶梯或下坡形状的主要原因是
12．已知一元二次方程
有一个根为零，则的值为
_
三、解答题（共34分）
1.解方程（每题4分，共16分）
| （1） （3）
|
（配方法） （2）
（ 因式分解法）
（求根公式法） （4）
（直接开方法）2.某城市为改善市容，绿化环境，计划经过两年使绿化面积增加44%，求这两年平均绿化面积的增长率（4分）.
3、（本小题8分）李栓身1.76，王鹏身高1.60，他们在同一时刻站在阳光下，李栓的影子长为1.10。
（1）求王鹏的影长。
（2）晚上，他俩又同时在同一路灯下，谁的影子长？
4、已知：如图，△ABC中，D是AB的中点，E是AC上一点，EF∥AB，DF∥BE。
（1）猜想：DF与AE有什么关系？证明你的猜想（5分）.
（2）若BE⊥AC，AD与DE有什么关系？证明你的结论（5分）.
5．宏达水果商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，出售价格每涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
答案：
选择题：DBDAB DBCCB
填空题
1. 2 2. 2 3.反比 4.平行四边形 5.2/5 6. a=8/b 曲线 一
7.0 8.小于1 9.2/3 10.10% 11.减小盲区 12.4/3
解答题
1. （1）X1=3根号5+6 2.X2=-3根号5+6
（2）X1=-1 X2=1/2
（3）X1=2 X2=-1/3
（4）X1=2 X2=-2
2.20%
3.（1）1米 （2）无法比较
4.（1）垂直 （2）相等
5. 5元