华师大九年级上期末试题(一)
一、选择题(每小题2分,共20分)
1、以下各式中正确的是( )
A、(a2)3=a5 B、a6÷a3=a2 C、(-1)0=-1 D、3-2=
2、把分式中的x和y都扩大3倍,则分式的值( )
A、扩大3倍 B、不 变 C、缩小3倍 D、扩大6倍
3、将一元二次方程![]() 配方后所得的方程是( )
配方后所得的方程是( )
A、(x-2)2=2 B、(x-1)2=2 C、(x-1)2=3 D、(x-2)2=3
4、化简分式的结果是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、代数式(x-3)(x+1)的值等于12,则x=( )
A、3或-1 B、-3或1 C、5或-3 D、3或-5
6、△ABC内接于⊙O,AB是直径,OD∥BC交AC于D,∠A=30°,AB=6cm,则OD=( )
A、3cm B、cm C、cm D、cm
7、口袋里有6个大小相同的乒乓球,其中2个为红色,1个为白色,3个为黄色,搅匀后从中摸出一个球是红色的概率是( )
 A、
B、
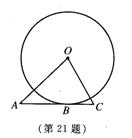
C、
D、
A、
B、
C、
D、
8、如图,AB=AC,AD=AE,要使△ABD≌△ACE,须补充条件( )
A、∠B=∠C B、∠D=∠E C、∠BAC=∠DAE D、∠CAD=∠BAC
9、两圆的半径分别是1和2,圆心距d=,则两圆的位置关系是( )
 A、相交 B、外切 C、内切 D、外离
A、相交 B、外切 C、内切 D、外离
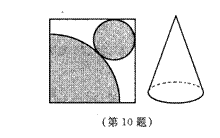
10、如图,在正方形铁皮上剪下一个圆和扇形(圆与扇形外切,且与正方形的边相切),使之恰好围成如图所示的一个圆锥模型,设圆半径为![]() ,扇形半径为R,则R与
,扇形半径为R,则R与![]() 的关系是( )
的关系是( )
A、R=2r B、R=4r C、R=2πr D、R=4πr
二、填空题(每小题2分,共24分)
11、使分式有意义的x的取值范围是________________。
12、方程x2=5x的解是_______________。
13、空气的单位体积质量约为0.00124![]() ,用科学记数法表示为___________
,用科学记数法表示为___________![]()
14、100件产品中,有2件次品,其余为正品,从中任取一件,取得正品的概率为_____。
15、代数式2x2+x与x2-x+3的值相等,则x=_____________。
16、如图,直线![]() 与
与![]() 垂直相交于O,以O为圆心作三个圆心圆(如图),已知大圆直径AB=2,则阴影部分面积为_______________。
垂直相交于O,以O为圆心作三个圆心圆(如图),已知大圆直径AB=2,则阴影部分面积为_______________。
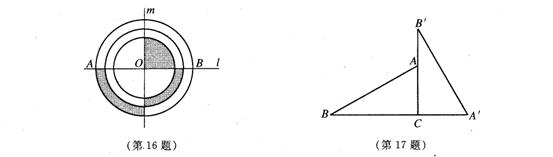
17、将Rt△ABC绕直角顶点C沿顺时针方向旋转90°得到△A′B′C′,已知BC=7cm,A′C=4cm,则AB′=__________cm。
18、计算(结果不含负指数):(a2b-3)-2=_________。
|
 19、如图,A、B、C、D是⊙O上的点,已知∠ACB=∠D=60°,AC=2cm,则△ABC的面积是___________cm2。
19、如图,A、B、C、D是⊙O上的点,已知∠ACB=∠D=60°,AC=2cm,则△ABC的面积是___________cm2。
20、如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,已知AB=6cm,则△DEB的周长是________cm。
21、如图,⊙O的半径是3,直线AC切⊙O于点B,已知AB=3,BC=,则∠AOC的度数是___________。
22、关于x的一元二次方程(m+1)x2+3x+m2-3m-4=0的一个根为0,则m=________。
三、解答题(第23题8分,第24题12分,第25、26题各5分,共30分)
23、计算:
⑴(-2a2b)3÷(-4a3b2); ⑵
24、用适当方法解方程:
⑴x2-2x-1=0 ⑵(x-2)2=5(2-x)
⑶
25、先化简,再求值:
(,其中x=
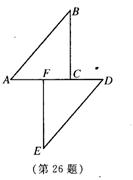
26、如图,BC⊥AD于C,EF⊥AD于F,AF=CD,AB∥DE,求证:AB=DE
四、作图题(不写作法,保留痕迹)(6分)
27、已知线段a,b。⑴作△ABC,使BC=a,AB=AC=b;
⑵分别作∠ABC、∠ACB的平分线BE、CF交于点P;
⑶连结AP并延长交BC于点D,观察AD是等腰△ABC的什么线?为什么?

五、解答题:(第28、30题各7分,第29题各6分,共20分)
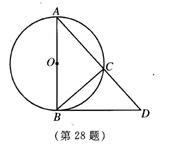
28、如图,AB是⊙O的直径,BC是弦,D在AC的延长线上,∠DBC=∠A,⑴试说明BD与⊙O的位置关系;⑵若⊙O的半径为5,BC=6,求AD的长。
29、某养鱼专业户搞池塘养鱼已三年,第一年放养鲢鱼苗20000尾,其成活率约为70%,在秋季捕捞时,随意捞出10尾鱼,称得重量如下表:
| 每尾重量(千克) | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 |
| 尾数 | 2 | 1 | 4 | 1 | 2 |
⑴根据样本平均数估计这塘鱼第一年的总产量是多少千克?
⑵已知市场售价为每千克4元,若把这塘鱼全部卖掉,除去当年提交成本16000元,头一年收入多少元?
⑶已知第三年收入达48400元,求第二、三年平均每年的增长率为多少?
30、如图,E是矩形ABCD的边BC延长线上的点,BE=BD,F是DE的中点,连接AF、CF
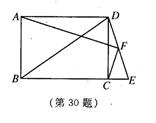 ⑴求证:∠BCF=∠ADF;
⑴求证:∠BCF=∠ADF;
⑵猜想∠AFC是锐角、直角还是钝角?证明你的猜想。
答案
1、 D;2、B;3、C;4、B;5、C;6、B;7、B;8、C;9、A;10、B
11、x≠1/2;12、x1=0,x2=5;13、1.24×10-3;14、98%;15、-3或1;16、π/4;17、3;18、![]() ;19、
;19、![]() ;20、6;21、75
;20、6;21、75![]() ;22、4;23、(1)
;22、4;23、(1)![]() (2)
(2)![]() ;24、(1)
;24、(1)![]() (2)
(2)![]() (3)
(3)![]() ;25、化简得
;25、化简得![]() ;值为
;值为![]() ;
;
26、略;27、(1)(2)略(3)三线答对一个即可;28、(1)略(2)12.5
29、(1)平均数为1(千克),1×20000×70%=14000(千克)
(2)4×14000-16000=40000(元)
(3)设平均增长率为x,40000![]() =48400
=48400
x=10%(x2=-2.1舍去)
30、(1)略
(2)直角。连结BF,则∠BFD=900,易证△ADF≌△BCF,得∠AFD=∠BFC,
故∠AFC=∠BFC+∠BFA=∠AFD+∠BFA=900