华师大九年级上期末试题（二）
一、填空题(每小题2分，共26分)
1、计算：a5÷a3＝______。
2、计算：(8x3－4x)÷(－2x)＝______。
3、已知：12个纳米的长度为0.米，用科学记数法表示该长度是______米．
4、已知：关于x的方程x2＋kx－2＝0的一个根是1，则k＝______ ．
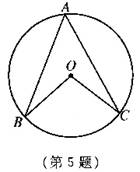
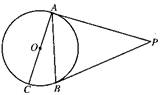
5、、如图，已知：点A在⊙O上，∠A＝50°，则∠BOC＝______度．
6已知：⊙O1与⊙O2的半径分别为5和2，O102＝7，则⊙O1与⊙O2的位置关系是______
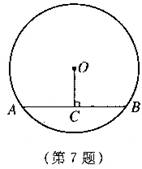
7、如图，已知：AB是⊙O的弦，OC⊥AB于C，AB＝8cm，OC＝3cm，则⊙O的半径是______cm。
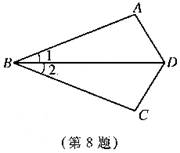
8、如图，已知：∠1＝∠2，现只需添加一个条件______就可使得△ABD≌△CBD．
9、抛掷一枚普通的正方体骰子，“出现点数为偶数”的概率为______。
10、某出租车公司在五一长假期间，平均每天的营业额为5万元，由此税务局以该公司每月营业额约为5×31＝155万元来制定今后每月纳税的标准，你认为这样做是否合理?_________
11、方程x2－2x＝0的解是______。
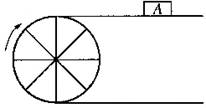
12、如图，当半径为18cm的转动轮转过150°角时，
传送带上的物体A平移的距离为___________cm．
13、某校去年对实验室器材的投资为2万元，预计
今、明两年的投资总额为8万元，若设该校今、明两
年在实验室器材投资上的平均增长率为x，则可列方程为___ ___。
二、选择题(每小题2分，共12分)
14、下列计算错误的是( )．
(A)()0＝1 (B)b3·b－2＝b (C)a－2＝ (D)(－1)－1＝1
15、用配方法解方程x2－4x－3＝0，应先化为( )．
(A)(x－2)2＝1 (B)(x－2)2＝7 (C)(x＋2)2＝1 (D)(x＋2)2＝7
16、下列命题中是假命题的是( )．
(A)三点确定一个圆
(B)三角形的内心到三角形各边的距离都相等
(C)在同一个圆内，同弧或等弧所对的圆周角相等
(D)在同一个圆中，相等的弧所对的弦相等
17、一布袋中装有红球5个、白球7个、绿球13个，它们除颜色外没有其他区别，若随机从袋中摸出一球，则不是白球的概率为(
)．
(A)7/25 (B)12/25 (C) 18/25 (D)4/5
18、如图，已知：PA、PB是⊙O的切线，A、B为切点，
AC是⊙O的直径，∠P＝40°，则∠BAC的度数是( )．
(A)10° (B)20° (C)30° (D)40°
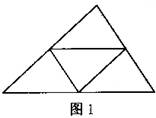
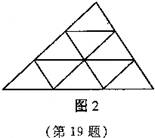
19、如图，将一个三角形的三边依次都分成2、3、4……等分，并将分点按图1、图2、图3那样连起来，这样，每个图中所得到的小三角形都会全等．按此方法，当三边都分成10等分时，所得到的全等小三角形的个数是( )．
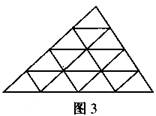
(A)98 (B)99 (C)1OO (D)101
三、解答题(共62分)
20、(6分)解方程：x2－2x－3＝0．
21、(6分)先化简再求值：(，其中x＝－2．
22、(6分)解方程：＝1
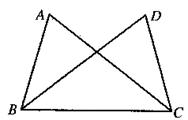
23、(6分)如图，已知：AB＝DC，AC＝DB，
求证：∠A＝∠D。
24、(6分)用尺规作图．(写出画法的主要步骤，并保留画图痕迹)
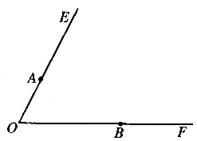
已知：∠EOF，点A、B分别在OE、OF上(如图)．
求作：点P，使点P到∠EOF的边OE、OF的距离相等，且PA＝PB．
25、(本题8分)如图，已知：AB是⊙O的直径，点C是⊙O上的一点，CD交AB的延长线于D，∠DCB＝∠ACO．
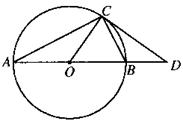(1)(5分)求证：CD是⊙O的切线；
(2)(3分)若CD＝4，BD＝2，求直径AB的长。
26、(本题9分)九年级6班有48名同学，其中男生30人．在一节数学课上，老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上，并放入一个盒子里摇匀．
(1)(3分)如果老师随便从盒子中取出一张小卡片，则每个同学被抽到的概率是多少?
(2)(3分)如果老师随便从盒子中抽出一张小卡片，那么抽到男同学的概率大还是抽到女同学的概率大?
(3)（3分)若老师已从盒子中抽出了10张小卡片，其中有4个是男同学，并把这10张小卡片放在一边，再从盒子中抽出第11张小卡片，则这时女同学被抽到的概率是多少?
27、(本题6分)某厂规定该厂家属区的每户如果一个月的用水量不超过m米3，则只需交10元水费，若超过规定的用水量，则这个月除仍要交10元水费外，超过部分还应按元／米3交费．
(1)(2分)该厂某居民2月份用水100米3，超过规定的用水量，则该户居民本月应交水费_______ __元；(用含m的代数式表示)
(2)(4分)下表是这户居民3、4月份的用水量和交水费情况：
| 月份 | 用水量(米3) | 交水费(元) |
| 3 | 80 | 25 |
| 4 | 48 | 10 |
根据上表，求该厂规定的m米3为多少?
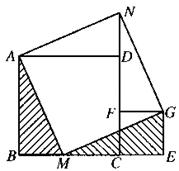
28、(本题9分)如图，已知：四边形ABCD、CEGF分别是边长为a、b(a＞b)的正方形，B、C、E三点在同一条直线上，点M在边BC上，且BM＝b，连接AM、MG，并将△ABM绕点A逆时针方向旋转到△ADN的位置，△MEG绕点G顺时针方向旋转后恰好与△NFG重合．
(1)(3分)求证：△ABM≌△MEG；
(2)(3分)求证：四边形AMGN是正方形；
(3)(3分)若正方形AMGN的边长为c，利用所给的图形能否证明“勾股定理”?若不能，请说明理由；若能，请写出证明过程．
答案
1、
；2、2－4x；3、1.2×10
；4、1；5、100；6、外切；7、5；8、答案不唯一，如AB=CB；9、50%；10、不合理；11、
；12、15π；13、
；
14、D；15、B；16、A；17、C；18、B；19、C；20；21、化简得2/x，值为－1；22、无解；
23、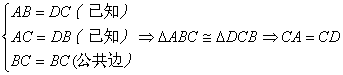
；24、略；25、（1）∵AB是直径，∴∠ACB=
。又∠DCB=∠ACO，∴∠OCD=∠OCB+∠BCD=∠OCB+∠ACO=∠ACB=，
∴CD是⊙O的切线。（2）AB=6
26、（1）1/48；（2）抽到男同学的概率大；（3）6/19
27、（1）10+
；（2）m=50O米
28、（1）ME=MC+CE=MC+BM+BC=AB，在Rt△ABM与Rt△MEG中，AB=ME，∠ABM=∠MEG=Rt∠，BM=EG，所以Rt△ABM≌Rt△MEG
（2）由（1）得AM=MG，又∵AM=AN，MG=NG，∴AM=MG=GN=AN，∴四边形AMGN是菱形，
∵∠BAM+∠AMB=Rt∠，∠BAM=∠EMG，∴∠EMG+∠AMB=Rt∠ ∴∠AMG+180
－（∠EMG+∠AMB）=90∴矩形AMGN是正方形。
（3）可以证明勾股定理