初三数学2004—2005学年度第一学期期末练习试卷
一．细心填一填（本大题共有12小题，15空，每空2分，共30分。请把结果0直接填在题中的横线上。只要你理解概念，仔细运算，积极思考，相信你一定会填对的！）
1．－3的相反数是 ；2的绝对值是 。
2．9的平方根是 ；16的算术平方根是 。
3．据新华社报道：2004年底在印度洋发生的大海啸已导致150 000人死亡，更是有不计其数的人家破人亡，这个数字用科学记数法可表示为 。
4．分解因式：3x2－3= 。
5．函数
中，自变量x的取值范围为
。
函数
中，自变量x的取值范围为
。
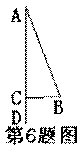
6．如图，在△ABC中，D是AC延长线上一点，∠A=360，∠B=620，则∠BCD= 。
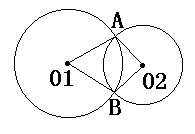
7．如图，⊙O1与⊙O2相交于A、B两点，顺次连结O1、A、O2、B，得到四边形O1AO2B。根据你所学过的矩形、菱形、正方形的性质时所获得的经验，试写出该四边形的一个性质 。
8．小明测得一周的体温并登记如下表：（单位0C）
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 | 周平均体温 |
| 体温 | 36.6 | 36.7 | 37.0 | 37.3 |
| 36.9 | 37.1 | 36.9 |
其中星期四的体温被墨迹污染，根据表中数据，你认为此日的体温为 0C
9．写出一个一元二次方程，它的一根x1为1，另一根x2的范围为－1< x2<1，该方程为 。
10．在一个看不见的口袋中，有3个红球，9个白球，1个黑球，若这些球的大小完全相同，且已搅拌均匀，小明准备从该口袋中摸两个红球，比较巧合的是他第一次刚好是取到了红球，那么小明再去摸球，他摸到红球的概率为 。
11．规定一种新运算：a※b=a2+b2－a－b.如3※4=32+42－3－4=18，那么4※6= 。
有两块同样大小且含600的直角三角板，把它们相等的边拼在一起（两块三角板不重叠），可以拼出 个四边形。
二、精心选一选（本大题共有8小题，每题3分，共24分。在每题给出的四个选项中，只有一项是符合题意的。把所选项前的字母代号填在题后的括号内。相信你一定会填对的！）
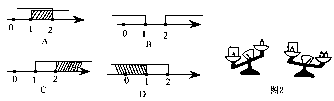
12．如图，天平右盘中的每个砝码的质量都是1g，则物体A的质量m（g）的取值范围，在数轴上可表示为 （ ）
13．下列属于最简二次根式的是 （ ）
A．
B．
C．
D．
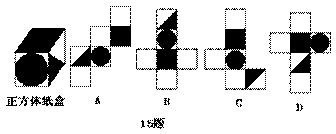
14．图中有一个正方体的纸盒，现用一把剪刀沿着它的棱剪成一个平面图形，则展开图应当是（ ）
15．如图，在一个棱长为10㎝的正方体的一个顶点处挖去一个棱长为1㎝的小正方体，那么剩余部分的表面积为 （ ）
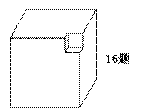
A300㎝ B. 599㎝ C. 601㎝ D.600㎝
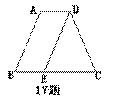
16．如图，等腰梯形ABCD中，AD//BC，AD=5，AB=6，BC=8。且AB//DE，那么△DEC的周长为 （ ）
A．3 B．12 C．15 D．19
17．下列黑体英文大写字母中，既是轴对称图形，又是中心对称图形的是 （ ）
A．E B.M C.N D.H
18．龟兔赛跑，它们从同一地点、同时出发不久兔子就把乌龟远远地甩在后面，于是兔子便得意洋洋地躺在一棵大树下睡起觉来，乌龟一直在坚持不懈、持之以恒地想终点跑着。兔子一觉醒来，看见乌龟快接近终点了，这才慌忙追赶下去。但最终输给了乌龟。下列图象中能大致反映龟兔行走的路程随时间变化情况的是 （ ）
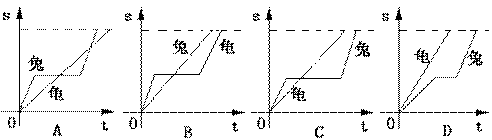
20。下列事件：确定事件是 （ ）
抛掷一枚六个面分别标有1～6的数字的均匀骰子，骰子停止转动后偶数点朝上。
从一副扑克牌中任意抽出一张牌，花色是红桃。
任意选择电视的某一频道，正在播放动画片。
在同一年出生的367名学生中，至少有两人的生日是同一天。
三、认真答一答（本大题共有7小题，满分58分。只要你认真思考，仔细运算，一定会解答正确的！）
21．（本大题共有3小题，每小题5分，共15分）
（1）计算：
（2）解不等式组：
（3）解方程组： 
22． （本题满分6分）
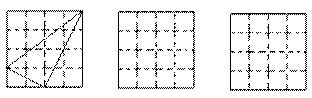
正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②连结3个格点，使之构成直角三角形。小华在左面的网格中作出了Rt△ABC。请你按照同样的要求，在右边的两个网格中，各画出一个直角三角形，并使三个网格中的直角三角形各不全等。
23.（本题满分8分）
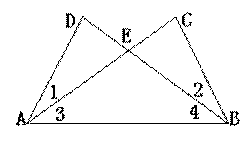
如图，给出下列论断：①DE=CE；②∠1=∠2；③∠3=∠4。请你将其中的两个作为条件，另一个作为结论。
请你写出一个正确的命题，并加以证明；
你还能写出这样的真命题吗？若有，请你再直接写出一对。
24.（本题满分6分）
某商场在促销期间，商场内所有商品按标价的80℅出售。同时当顾客消费满一定的金额后，按如下方案获得相应金额的奖励：
| 消费金额a（元） | 200≤a＜400 | 400≤a＜500 | 500≤a＜700 | 700≤a＜900 | … |
| 获得奖券的金额（元） | 30 | 60 | 100 | 130 | … |
根据上述促销方法，顾客在商场内购物可以获得双重的优惠。例如：标价为450元的商品，消费金额为450×80℅=360，获得的优惠额为450×（1－80℅）+30=120元。设购买该商品得到的优惠率=购买该商品得到的优惠额÷商品的标价。
购买一件标价为1000元的商品，顾客得到的优惠额是多少？
对标价在500～800元（含500元和800元）之间的商品，顾客购买标价为多少元的商品，可以得到1/3的优惠率？
25.（本题满分6分）
为了从甲、乙两名学生中选拔一人参加六月份的全市中学生数学竞赛，每个月对他们的学习水平进行一次检测，下图是两人赛前5次测验成绩的折线统计图。
分别求出甲乙两名学生5次测验成绩的平均数和方差；
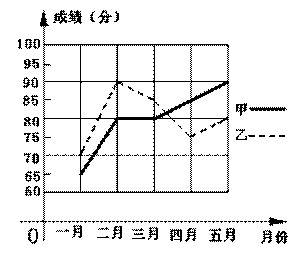如果你是他们的辅导老师，应选派哪一名学生参加这次数学竞赛，请结合所学统计知识
说明理由。
26.（本题满分7分）
父亲和儿子同时出 去晨练，如图①，实线表示父亲离家的路程y(米)与时间x（分钟）的函数图象；虚线表示儿子离家的路程y（米）与时间x（分钟）的函数图象，由图象可知，他们在出发10分钟时第一次相遇，此时离家400米；晨练了30分钟，他们同时到家。
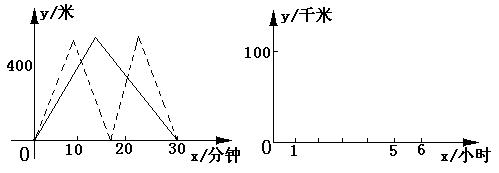
根据阅读材料给你的启示，利用指定的直角坐标系（如图②）或用其他方法解答问题：
一巡逻艇和一货轮同时从A港口前往100千米外的B港口，巡逻艇和货轮的速度分别为每小时100千米和每小时20千米，巡逻艇不停地往返于A、B两港口（巡逻艇调头的时间忽略不计）。
（1） 货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次；
（2） 出发多少时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？
28.（本题满分10分）
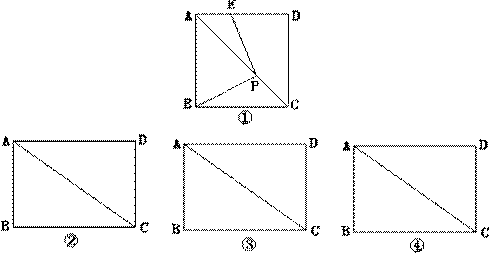
（1）.如图将一把三角尺放在正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与线段DA相交于点E，求证：PB=PE。
（2）.操作：如图，已知矩形ABCD，AD=4，DC=3。
将一把三角尺放在矩形ABCD上，并使它的直角顶点P在对角线上滑动，直角的一边始终经过B点，另一边与线段DA相交于点E。
探究①PB=PE吗？如果相等，请说明；如果不相等，请求出PB︰PE的值。
②设点P‘分别滑动到P1、P2时，所对应的三角形分别是△BP1E1、△BP2E2，试判断这两个三角形是否相似，请证明你的结论。（图②、③供操作，图④备用）
29、动脑想一想（本大题共有2小题，共18分，只要你认真探索，仔细思考，你一定会获得成功的！）
（本题满分8分）
在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案。也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里面叫平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时，就拼成了一个平面图形。
根据下列图形，填写表中空格：
| 正多边形变边数 | 3 | 4 | 5 | 6 | … | n |
| 正多边形每个内角的度数 |
|
| … |
如果限用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？
从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？并说明你的理由。
30.（本题满分10分）
已知一次函数y1=2x，二次函数y2=x2+1.
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
| x | －3 | －2 | －1 | 0 | 1 | 2 | 3 |
| y1=2x | |||||||
| y2=x2+1 |
（Ⅱ）观察第（Ⅰ）问中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数对应的函数值y1≤y2成立；
（Ⅲ）试问，是否存在二次函数y3＝ax2+bx+c,其图像经过点（－5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立，若存在，请求出该二次函数的解析式；若不存在，请说明理由。