九年级（上）期末试卷(4)华师大版

　 初三数学2004—2005学年度第一学期期末练习试卷

　

一、细心填一填（本大题共12题，15空，每空2分，共30分）

1、氧原子的直径约为0.m，用科学记数法表示为　　　　　　 。

2、已知分式，当x=2时，分式无意义；当x=4时，分式的值为零，则b^a=　　　。

第19题

3、计算：（1）÷4x·=　　，（2）（a^-3）²(ab²)^-3=　　　。(结果化为正整数指数幂)

4、已知x=2是方程x²-3x+m=0的一个根，则方程的另一个根是　　  ，m=　　　　。

第18题

5、写出一个两实数根之和为2的一元二次方程　　　　　　　　  。

第20题

6、若矩形的长和宽分别是方程4x²-12x+3=0的两个根，则矩形的周长是　　，面积是　 。

7、若⊙O的半径为4㎝，弦AB=4㎝，则弦AB所对的圆周角是　　　　  °。

8、圆锥的底面半径为1，表面积为4π，则圆锥的母线长为　　　　  。

9、已知AB是⊙O的直径，AB=16㎝，P是OB的中点，弦CD过点P，∠APC=30°，则CD=　　　　。

10、为了测量一个圆形铁环的半径，小华采用了如下方法：将铁环平放在水平桌面上，用一个锐角为30°的直角三角板和一个刻度尺，按如图所示的方法得到有关数据，进而求得铁环的半径，若测得AB=10㎝，则铁环的半径是　　　　  。

第11题

11、如图，△ABC是等边三角形，D、E分别在BC、AC上，且BD=CE，AD、BE相交于点P，则∠APE=　　　　。

12、已知y₁=2x,y₂=,y3=，…，则y₁·y₂₀₀₄=　　。

二、心选一选（本大题共8小题，每题3分，共24分）

13、下列各式中，运算正确的是（　　）

 A、a²·a³=a⁶　 B、()^-2+200⁰=4　　　C、(-)²= 　　  D、-21a²b³c÷3a²b=-7b²

14、要使分式（－ ）÷的值是负整数，则a应取的数为（　　）

 A、1和2　　　　　　 B、2和3　　　　　　 C、a＞1　　　　　　　 D、a＞2

15、若一元二次方程（a-1）x²+2x-3=0有两个实数根，则a的取值范围是（　　）

 A、a＞　　　　　　 B、a≥　　　　　　 C、a＞且a≠1　　　　 D、a≥且a≠1

16、利用尺规作图不能唯一作出三角形的是（　　）

 A、已知三边　　　　　　　 B、已知两边及夹角　　　　　

 C、已知两角及夹边　 D、已知两边及其中一边的对角　　　　　　　　　　　　　　　　　　　　

17、在直角坐标系中，⊙O的圆心在原点，半径为3，⊙A的圆心A的坐标为（-，1），半径为1，那么⊙O与⊙A的位置关系是（　　）

 A、外离　　　　　　　 B、外切　　　　　　　 C、内切　　　　　　　 D、相交

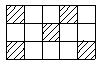
18、一只小狗在如图的方砖上走来走去，最终停在阴影方砖上的概率是（　　）

 A、　　　　 B、　　　　　 C、　　　　　 D、

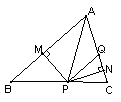
19、如图，在不等边三角形ABC中，AQ=PQ，PM⊥AB，PN⊥AC，PM=PN，下面给出的结论：①AN=AM ②QP∥AM ③△ABC∽△QNP，其中正确的是（　　）

 A、①②③　　　　　 B、仅①和②　　　　　　　 C、仅②和③　　　　　　　 D、仅①　　　

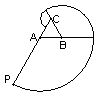20、如图，有一个边长为6㎝的正三角形ABC木块，点P是边CA的延长线上的点，在A、P之间拉一条细绳，绳长AP为15㎝，握住点P，拉直细绳，把它全部紧紧缠绕在△ABC木块上（缠绕时木块不动）。若圆周率取3.14，则点P运动的路线长为（精确到0.1㎝）（　　）

 A、28.3㎝　　　　　 B、28.2㎝　　　　　 C、56.5㎝　　　　　 D、56.6㎝　　　　　

三、认真答一答

21、本题共16分，每题4分。

（1）计算：+2（3.14-π）⁰-（-1）^-2003+ 　　（2）计算：+

第10题

（3）解方程：- = 　　　　　　　　　　　　 （4）解方程：2x=3x²-4

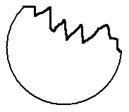22、(本题6分)已知一面圆形镜子不慎落地，其中一块碎片如图所示，怎样才能确定这面镜子的半径呢？（利用尺规作图解题，保留作图痕迹）。

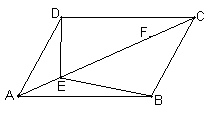
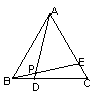
23、（本题6分）如图，在　 ABCD中，点E、F在对角线AC上，且AE=CF，请你以F为一个端点和图中已表明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。

（1）连结　　　　 ；

（2）猜想：　　  = 　　；

（3）证明：

24、（本题7分）已知关于ｘ的方程x²-2(m+1)x+m²=0，（1）当m取什么值时，原方程没有实数根？（2）对ｍ选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和。

	（1）

25、（本题7分）去年３月18号，我校师生到离校15千米的江阴鹅鼻嘴公园春游，先遣队与大队同时出发，行进速度是大队的1.2倍，以便提前15分钟到达目的地做准备工作，求先遣队和大队的速度各是多少？

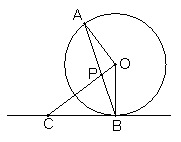26、（本题7分）如图，AB是⊙O的弦，CO⊥OA，OC交AB于点P，且PC=BC，BC是⊙O的切线吗？为什么？

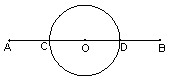
27、（本题8分）在相距40千米的A、B两市间有一个半径为10千米的近似圆形的湖泊，湖泊的圆心恰好在A、B的连线的中点处，现要绕过湖泊从A市到B市去，路程要尽量短，请你设计三种行走路线，并比较哪一种路线最近？为什么？（不考虑造桥，下图（1）（2）（3）供设计画图用，用实线画出设计路线并算出路线长）。

（3）

（2）

　 　　

四、动脑想一想

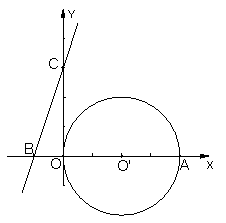
28、（本题9分）如图，在直角坐标系中，点O’的坐标为（2，0），圆O’与x轴交于原点O和点A，又B、C、E三点坐标为（-1，0）、（0，3）、（0，b），且0＜b＜3。（1）求点A的坐标和经过B、C两点的直线解析式。（2）当点E在线段OC上移动时，直线BE与⊙O有哪几种位置关系？求出每种关系时b的取值范围。

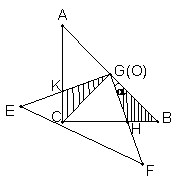
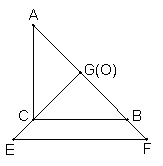
29、（本题10分）把两个全等的等腰直角三角板ABC和EFG（其直角边长均为4）叠放在一起（如图1），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合。现将三角板EFG绕O点按顺时针方向旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图2）。

（1）　　　 在上述过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；

（2）　　　 连接HK，在上述旋转过程中，设BH=x，△GKH的面积为y,求y与x之间的函数关系式，并写出自变量x的取值范围；

（3）　　　 在（2）的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时x的值；若不存在，说明理由。

			图2
	图1