初三数学2004—2005学年度第一学期期末练习
注意事项及说明: 本卷考试时间为120分钟, 全卷满分为130分.
| 题号 | 一 | 二 | 三 | 四 | 总分 | |||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | ||||
| 得分 | ||||||||||||
一． 细心填一填（本大题共有12小题，15个空，每空2分, 共30分. 相信你会填对的!）
1．9的平方根是_________，-3的倒数为___________．
2．一种细菌的半径是0.00004米，用科学计数法表示出来是_________．
3．实数范围内分解因式得a4－4a2+4=_______________________________.
4．方程
的根是____________；(x-2)x=3(x-2) 的根是_____________．
5．已知
是整数，点
在第二象限，则= ．
6．如图，P是⊙O外一点，PA、PB分别和⊙O切于A、B，C是弧AB上任意一点，
过C作⊙O的切线分别交PA、PB于D、E，若△PDE的周长为 12，
则PA长为______________．
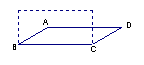7. 如图，若将四根木条钉成的矩形木框变为平行四边形ABCD的形状，
并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值 等于
．
8.在半径为1的⊙O中，弦AB、AC分别是
和
， 则∠BAC
的度数为 ．
9. 分析图①,②,④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分.
10. 命题“等腰三角形两腰上的高相等”的题设是
结论是
11. 一个圆锥的侧面积是底面积的2倍,则这个圆锥的侧面展开图(扇形)的圆心角是
__ 度.
12．扑克牌游戏：小明背对小亮，让小亮按下列四个步骤操作：
第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌现有的张数相同；
第二步 从左边一堆拿出两张，放入中间一堆；
第三步 从右边一堆拿出一张，放入中间一堆；
第四步 左边一堆有几张，就从中间一堆拿几张牌放入左边一堆。
这时，小明准确说出了中间一堆牌现有的张数。你认为中间一堆牌现有的张数是 ．
二． 精心选一选（本大题共有8小题，每小题3分，共24分. 注意每小题所给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填在题后的括号内. 相信你一定会选对！）
13．下列运算正确的是 （ ）
A.6a6÷3a3=2a2 B.2-2=-4 C.(a+1)0=0 D.(-2x2y)÷0.5xy=-4x(02长沙市)
14． 如图，在方格纸中有四个图形<1>、<2>、<3>、<4>，其中面积相等的图形是（ ）
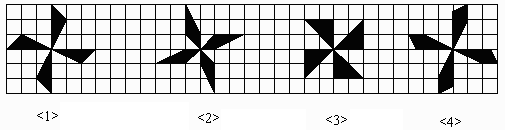
A. <1>和<2> B. <2>和<3> C. <2>和<4> D. <1>和<4>
15、实验中学初三年级进行了一次数学测验，参考人数共540人，为了了解这次数学测验成绩，下列所抽取的样本中较为合理的是 （ ）
A．抽取前100名同学的数学成绩
B．抽取后100名同学的数学成绩
C．抽取（1）、（2）两班同学的数学成绩
D．抽取各班学号为3号的倍数的同学的数学成绩
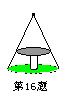16. 如图：这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图，已知桌面的直径为1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为
（ ）
A、
平方米 B、
平方米
C、
平方米
D、
平方米
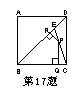
17. 如图：E是边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是 （ ）
A、
B、
C、
D、
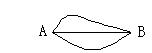
18.已知,如图,A,B两村之间有三条道路,甲,乙两人分别从A,B两村
同时出发,他们途中相遇的概率为 ( )
A、 
B 、
C、 
D、
19． (02长沙市)下列命题正确的是 （ ）
A、对角线相等的四边形是矩形 B、相邻的两个角都互补的四边形是平行四边形
C、平分弦的直径垂直于弦，并且平分弦所对的两条弧 D、三点确定一个圆
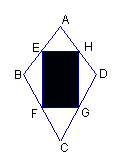
20.某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料，生产一批
形状如右图的风筝，点E、F、G、H分别是四边形ABCD各边的中点，
其中阴影部分用甲种布料，其余部分用乙种布料（裁剪两种布料时，
均不计余料）。若生产这批风筝需要甲种布料30匹，那么需要乙种
布料 （ ）
A、15匹 B、20匹 C、30匹 D、60匹
三． 认真答一答(本大题共有7小题, 共58分. 只要你认真思考, 仔细运算, 一定会解答正确的!)
21．计算：(每小题6分)
（1）计算：
（２）解方程：
（３）先化简，再求值：
，其中
 |
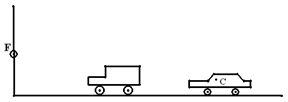22．（本题4分）(1)如图，F表示一路口交通信号灯的位置，一小汽车停在一货车后面，点C表示小汽车司机头部。问若小汽车司机抬头向正前方望去，他能否看到信号灯F，为什么？
23．（本题7分）已知关于x的方程x2－2(m+1)x+m2=0.
（1）当m取什么值时，原方程没有实数根；
（2）对m选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和.
24. （本题6分） 已知A={3，4}，B={3，6，9}，C={3，12}。其中它们分别表示包含这些线段长度的集合，如果从集合A中随机选取一个长度，从集合B中随机选取一个长度，从集合C中随机选取一个长度，请回答下列问题：
（1）以选取的三个长度的线段为边，能构成三角形的概率是多少？
（2）以选取的三个长度的线段为边，能构成等腰三角形的概率是多少？
（3）以选取的三个长度的线段为边，能构成等边三角形的概率是多少？
25. （本题9分）如图，两种规格的钢板原料，图（1）的规格为1m×5m，图（2）是由5个1m×1m的小正方形组成。电焊工王师傅准备用其中的一种钢板原料裁剪后焊接成一个无重叠无缝隙的正方形形状的工件（不计加工中的损耗）.
（1） 焊接后的正方形工件的边长是
（2） 分别在图（1）和图（2）中标出裁剪线，并且画出所要求的正方形形状的工件示意图（保留要焊接的痕迹）；
（3） 从节约焊接材料的角度，试比较选用哪种原料较好？
（1） （2）
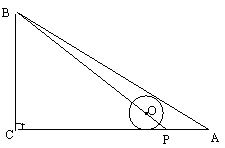
26. （本题6分）如图2，在ΔABC中，∠C＝90°，AC＝8，AB＝10，点P在AC上，AP＝2，若⊙O的圆心在线段BP上，且⊙O与AB、AC都相切，求 ⊙O的半径．
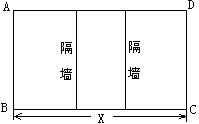
27. （本题8分） 某工厂拟建一座平面图形为矩形且占地面积为２００平方米的三级污水处理池（如图）由于地形限制，三级污水处理池的长、宽都不能超过１６米。如果池的外围墙建造单价为每米４００元，中间两道隔墙建造单价为每米３００元，池底建造单价为每平方米８０元（池墙的厚度忽略不计）.
（１） 当三级污水处理池的总造价为４７２００元时，求池长x;
（２）
如果总造价越低越合算，那么根据题目提供的信息，以４７２００元为总造价修建三级污水处理池是否最合算？请说明理由.
四．仔细想一想（本大题共有２小题， 共１８分. 只要你仔细探索，你一定会成功！）
28．（本题8分） 观察——度量——证明
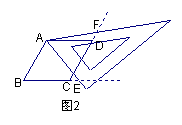
用两个全等的等边三角形⊿ABC、⊿ACD拼成菱形ABCD。把一个含60º角的三角尺与这个菱形叠合，使三角尺的60º角的顶点与点A重合，两边分别与AB、AC重合.将三角尺绕点A按逆时针方向旋转.
（1） 当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时（如图1），通过观察或测量BE、CF的长度，你能得出什么结论？并证明你的结论.
（2） 当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时（如图2），你在（1）中得到的结论还成立吗？简要说明理由．
 |  | ||
29. （本题10分）
已知Rt△ABC中，∠C＝90°，AC=3，BC=4，点E在AC上，E与A、C均不重合.
（1） 若点F在AB上，且EF平分Rt△ABC的周长，设AE=x，用含x的代数式表示S△AEF：
（2） 
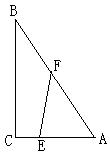若点F在折线ABC上移动，是否存在直线EF将Rt△ABC的周长与面积同时平分？若存在，求出AE的长；若不存在，请说出理由.