初三数学 2004—2005学年度第一学期期末练习试卷
一、细心填一填：（本大题共有14题，15空，每空2分，共30分。请把结果直接填在题中的横线上。只要你理解概念，仔细运算，积极思考，相信你一定会填对的！）
1、―5的相反数的倒数是 。
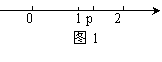
2、实数p在数轴上的位置如图1所示，化简
= 。
 |
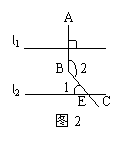3、如图2，直线l1∥l2，AB⊥l1，垂足为O，BC与l2相交于点E，若∠1=43°，
则∠2= °。
4、函数
的自变量
的取值范围是
；
当=
时，代数式
的值为零。
5、一种细菌的半径是0.00004m，用科学记数法把它表示为 m。
6、乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排 种不同的车票。
7、已知圆锥的底面直径为4，母线长为6，则它的侧面积为 。
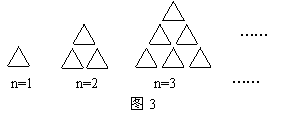8、如图3，是用火柴棍摆出的一系列图案。按这种方式摆下去，当每边摆20（n=20）根时，需要的火柴棍总数为
根。
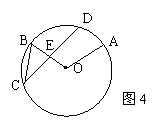9、如图4，A、B、C、D是⊙O上四点，且D是弧AB的中点，CD交OB于E，∠AOB=100度，∠OBC=55度，则∠OEC= 度。
10、一次函数的图象过点（1，2），且
随的增大而增大，则这个函数的解析式是
。（任写一个）
11、已知抛物线
的图象与轴有两个交点，那么一元二次方程
的根的情况是
。
12、若
，计算
=
。
13、某商品的进价是500元，标价为750元，商店要求的利润率不低于5%的售价打折出售，售货员最低可以打 折出售此商品。
14、若点P（a+b，―5）与（1，3a―b）关于原点对称，则关于的二次三项式
可以分解为
。
二、精心选一选：（本大题共8小题，每题3分，共24分。在每题所给出的四个选项中，只有一项是符合题意的，把所选项的字母代号填在题后的括号内。相信你一定会选对的！）
15、下列计算正确的是………………………………………………………………（ ）
A．
B．
C．
D．
16、关于的一元二次方程
有两个不相等的实数根，则m的取值范围是……………………………………………………………………………………（ ）
A．m>1 B．m<1 C．m>―1 D．m<―1
17、某超市一月份的营业额为200万元，三月份的营业额为288万元，如果每月增长的百分数相同，则平均每月的增长率是……………………………………………………（ ）
A．10% B．15% C．20% D．25%
18、下列图案中，有且只有三条对称轴的是………………………………………（ ）
A． B． C． D．
19、下面是空心圆柱在指定方向上的视图，正确的是……………………………（ ）
 |
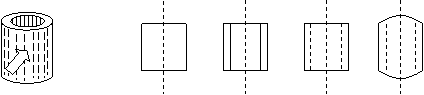A． B． C． D．
20、用两个全等的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③菱形；④正方形；⑤等腰三角形。一定可以拼成的图形是…………………………………………………（ ）
A．①②⑤ B．②③⑤ C．①④⑤ D．①②③
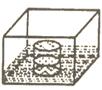
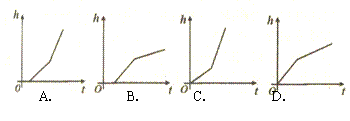21、如右图，向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽。水槽中水面上升高度h与注水时间t之间的函数关系，大致是下列图象中（ ）
22、明明的书柜中有很多书，妈妈让明明把书分类，其中四分之一是故事书，二分之一是学习用书，五分之一是科学探险书，剩下的都是科普等其它书籍。若这些书是任意摆放的，那么从中抽取一本书是故事书的机会是……………………………………………………（ ）
A．
B．
C．
D．不能确定
三、认真答一答：（本大题共7小题，满分58分。只要你认真思考，仔细运算，一定会解答正确的！）
23、（本题共3小题，每小题5分，共15分）
（1）计算：
（2）解不等式：
（3）解方程组：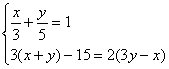
24、（本题满分6分）在如图的12×24的方格纸中（每个小方格的边长都是1个单位）有一△ABC。现把△ABC分别向右、向上平移8个单位和3个单位得到△A1B1C1；再以点O为旋转中心把按顺时针方向旋转90°得到△A2B2C2。请在所给的方格纸中作出△A1B1C1和△A2B2C2。
 |
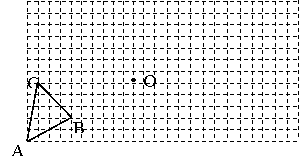25、（本题满分8分）如图，AB=CD，AC=BD。找出图中所有的全等三角形，并说明理由。
 |
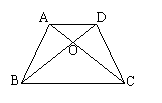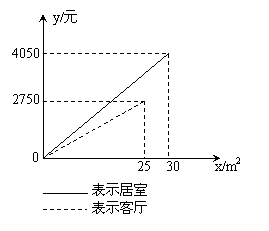26、（本题满分6分）小亮家最近购买了一套住房，准备在装修时用木质地板铺设居室，用瓷砖铺设客厅，经市场调查得知，用这两种材料铺设地面的工钱不一样，小亮根据地面的面积，对铺设居室和客厅的费用（购买材料费用和工钱）分别作了预算，通过列表，并用/m2表示铺设地面的面积，用/元表示铺设费用，制成右图。请你根据图中所提供的信息，解答下列问题。
（1）预算中铺设居室的费用为 元/m2；铺设客厅的费用为 元/m2；
（2）表示铺设居室的费用/元与面积/m2之间的函数关系为
；
（3）已知在小亮的预算中，铺设1 m2的瓷砖比铺设1 m2的木质地板的工钱多5元，购买1 m2的瓷砖是购买1 m2木质地板费用的
，那么铺设每平方米木质地板、瓷砖的工钱各是多少元？购买每平方米的木质地板、瓷砖的费用各是多少元？
27、（本题满分6分）报纸上刊登了一则新闻，标题为“保健食品合格率75%”，请据此回答下列问题。
（1）这则新闻是否说明市面上所有保健食品中恰好有25%为不合格产品？
（2）你主为这则消息来源于普查，还是抽样调查？为什么？
（3）如果已知在这次质量监督检查中各项指标均合格的商品有45种，你能算出有多少种保健食品接受检查了吗？
（4）此次商品质量检查的结果显示如下表，有人由此认为：“进口商品的不合格率较低，更让人放心。”你同意这种说法吗？为什么？
| 产 地 | 同 内 | 进 口 |
| 被 检 数 | 55 | 5 |
| 不合格数 | 14 | 1 |
28、（本题满分8分）某校的校门是一抛物线形水泥建筑物，如图所示，大门的地面宽度为8m，两侧距地面4m处各有一个挂校名横匾用的铁环，两铁环的水平距离为6m。
（1）求校门的高为多少米（水泥建筑物的厚度不计）？
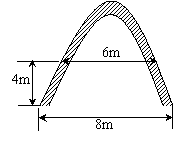（2）由于学校正在改善办学条件，有一高5m、宽5m的大型工程车需进入校园，问该车能否顺利从校门通过？
29、（本题满分9分）如图5，⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在弧AB上取一点D，分别作直线CD、ED，交直线AB于点F、M。
（1）求∠COA和∠FDM的度数；
（2）求证：△FDM∽△COM；
（3）如图6，若将垂足G改取为半径OB上任意一点，点D改取在弧EB上，仍作直线CD、ED，分别交直线AD于点F、M。试判断：此时是否仍有△FDM∽△COM？证明你的结论。
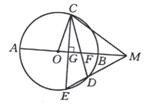
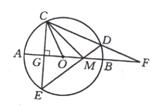
图5 图6
四、动脑想一想：（本大题菜有2小题，共18分。只要你认真探索，仔细思考，你一定会获得成功的！）
30、（本题满分8分）已知：四边形ABCD中，AB∥CD，且AB、CD的长是关于的方程
的两个根。
（1）当m=2或m>2时，四边形ABCD分别是哪种四边形？请说明理由。
（2）若M、N分别是AD、BC的中点，线段MN分别交AC、BD于点P、Q，PQ=1且AB<CD，求AB、CD的长。
（3）在（2）的条件下，AD=BC=2，求一个一元二次方程，使它的两个根分别是tan∠BDC和tan∠BCD。
31、（本题满分10分）已知：等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h。若点P在一边BC上（如图7），此时h3=0，可得结论：h1+h2+h3=h。请直接应用上述信息解决下列问题：当点P在△ABC内（如图8）、点P在△ABC外（如图9）这两种情况时，上述结论是否成立？若成立，请给予证明；若不成立，h1、h2、h3与h之间又有怎样的关系，请写出你的猜想，不需要证明。
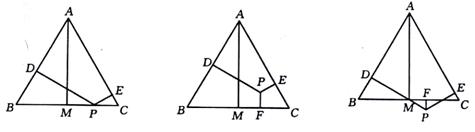
图7 图8 图9