九年级数学（上）期末试题
姓名： 成绩：
一、 填空题：（耐心填一填，你一定能填好！每空3分，共36分）
1、（
）0=
；（
）-2= 。
2、函数y=
中自变量x的取值范围是 。
3、当m= 时，方程
是一元二次方程。
4、如果方程3x2+x+a=0有实数根，则a的取值范是 。
5、方程x2+5x-m=0的一个根是2，则m= ；另一个根是 。
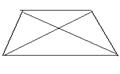6、等腰梯形ABCD中，AB∥CD,对角线AC与BD相交与O,请写出图中一对相等的线段
。 D C 7、正方形ABCD的边长是2cm,以直线AB为轴旋转一周，所得 O
到的圆柱的侧面积为 cm2. A B
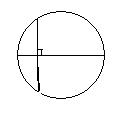
8、如图、AB是⊙O的直径，弦CD⊥AB,垂足为P，如AP∶PB=1∶4,CD=8,则AB= .
C
A P O B(8题)
(9)
D
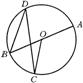
9、如图，在⊙O中，AB是⊙O的直径，∠D＝40°，则∠AOC的度数为_____ _
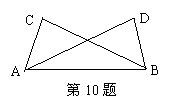
10、如图,已知AC=BD,则再添加条件 ,可证出△ABC≌△BAD.
二、选择题：（精心选一选，你一定能选准！3×10=30分）
1、下列运算正确的是( )
A、 
B、 
C、 
D、 
2、计算
的结果是( )
(A)
(B)
(C)
(D)
3、关于
的一元二次方程
的一个根是0，则
的值为（ ）
（A）1 （B）
（C）1或 （D）0.5
4、如图，两个标有数字的轮子可以分别绕轮子中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字，这两个数字和为偶数的概率是（ ）
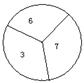
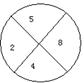（A）
（B）
（C）
（D）
5、下列说法正确的是（ ）
（A）三点确定一个圆。 （B）一个三角形只有一个外接圆。
（C）和半径垂直的直线是圆的切线。 （D）三角形的内心到三角形三个顶点距离相等。
6、关于的方程
有两个不相等的实数根，则
的取值范围是（ ）
A．
B．
C．
D．
7、下列五个命题：（1）若直角三角形的两条边长为5和12，则第三边长是13；
（2）
＝a（a≥0）；（3）若点P（a，b）在第三象限，则点P＇（－a，－b+1）在一象限；（4）对角线互相垂直且相等的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等。 其中正确命题的个数是（ ）
A．2个 B．3个 C．4个 D．5个
8、若圆锥的母线长为4cm，底面半径为3cm，则圆锥的侧面展开图的面积是（ ）
（A）
； （B）
； 
（C）
； （D）
；
9、一个直角三角形斜边长为
，内切圆半径为
，则这个三角形周长是（ ）
A、
B、
C、
D、
10、下列说法错误的是（ ）
A、顶角和腰对应相等的两个等腰三角形全等B、顶角和底边对应相等的两个等腰三角形全等C、斜边对应相等的两个等腰直角三角形全等 D、两个等边三角形全等
三、解答题：（细心做一做，你一定行！66分）
1、（6分）计算: 
2、（6分）解方程：x2+2x-3=0。
3、解方程：
（6分） 4、解方程
（6分）
5、化简：
（6分）
6、（8分）已知：关于x的方程x2-kx-2=o①、求证：方程有两个不相等的实数根。②、设方程的两个根为x1,x2如果2（x1+x2）>x1x2,求k的取值范围。
|
 | |||
 | |||
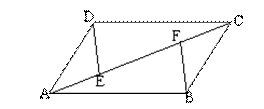8、（6分）如图，在平形四边形ABCD中，E、F是对角线AC上的两点，且AE=CF。求证：DE=BF
9、（6分）一布袋中有红、黄、白三种颜色的球各一个，它们除颜色外其它都一样。小亮从布袋中摸出一个球后放回去摇匀，再摸出一个球。请你利用列举法（列表或画树状图）分析并求出小亮两次都能摸到白球的概率。
10、（8分）同一底上的两底角相等的梯形是等腰梯形吗？如果是，请给出证明（要求画出图形，写出已知、求证、证明）；如果不是，请给出反例（只需画图说明）.
11、（8分）如图8，PA切⊙O于点A，PBC交⊙O于点B、C，若PB、PC的长是关于x的方程
的两根，且BC=4，求（1）m的值；（2）若PA2=PB•PC，求PA的长；
12、（10分）今年五月，某工程队（有甲、乙两组）承包人民路中段的路基改造工程，规定若干天内完成．（1）已知甲组单独完成这项工程所需时间比规定时间的2倍多4天，乙组单独完成这项工程所需时间比规定时间的2倍少16天．如果甲、乙两组合做24天完成，那么甲、乙两组合做能否在规定时间内完成？（2）在实际工作中，甲、乙两组合做完成这项工程的
后，工程队又承包了东段的改造工程，需抽调一组过去，从按时完成中段任务考虑，你认为抽调哪一组最好？请说明理由．
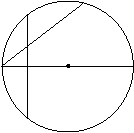
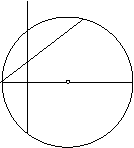
13、（12分) 如图，AB、AC分别是⊙O的直径和弦，D是劣弧AC的中点，DE⊥AB于H，交⊙O于点E，交AC于点F．
（1） 图中有哪些必相等的线段？（要求：不要标注其它字母，找结论的过程中所作的辅助线不能出现在结论中，不必写出推理过程．）
（2） 若过C点作⊙O的切线PC交ED延长线于P点，（请补全图形），
求证：PF2=PD·PE；
（3） 已知AH＝1，BH＝4，求PC的长． C
D
F
A H O B
E
答案：
一、填空题：
1、1，9； 2、x≤5且x≠-1; 3、m=3; 4、a≤
; 5、14，-7；6、AC=BD; 7、8
8、10； 9、100° 10、∠CAB=∠DBA
二、 选择题：BBBCADABBD
三、 解答题：
1、4-8×0.125+1+1=5
2、（x-1）(x+3)=0 x1=1,x2= -3 3、3x2+x-2=0 x1=
-1,x2=
4,3(x-1)-(x+3)=0 2x-6=0 x=3,经检验是圆方程的解。
5、
6、①、Δ=k2+8 ∵k2≥0 ∴k2+8>0.∴方程有两个不相等的实数根。
②、∵x1+x2=k,x1x2= -2 ∴2k>-2 ∴k>-1
7、略 8、∵平行四边形ABCD∴AD=BC,DC∥AB,∴∠DAE=∠BCF,AE=CF.∴ΔDAE≌ΔDAF,∴DE=CF.
9、
10、是等腰梯形……………………………………………………………………………………（1分）
已知：梯形ABCD，AD∥BC且∠B=∠C（或∠A=∠D）………………………………（2分）
求证：梯形ABCD是等腰梯形……………………………………………………………（3分）
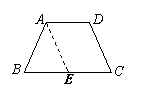证明一：过点A作AE∥DC，交BC于E…………………………（4分）
∵AD∥BC AE∥DC
∴四边形AECD是平行四边形，∴∠AEB=∠C，
AE=DC…………………………………………………（5分）
∵∠B=∠C
∴∠AEB=∠B………………………………………………………………………（6分）
∴AB=AE……………………………………………………………………………（7分）
∴AB=DC
∴梯形ABCD是等腰梯形………………………………………………………（8分）
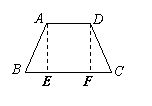
证明二：过A、D两点分别作AE⊥BC，DF⊥BC垂足为E、F
∵AE⊥BC、DF⊥BC
∴AE∥DF且∠AEB=∠DFC
∵AD∥BC
∴四边形AEFD是平行四边形 ∴AE=DF
∵∠AEB=∠DFC ∠B=∠C
∴△AEB≌△DFC ∴AB=DC
∴梯形ABCD是等腰梯形
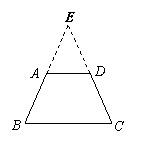
证明三：延长BA、CD交于E点
∵∠B=∠C ∴BE=CE
∴AD∥BC ∴∠EAD=∠B，∠EDA=∠C ∴∠EAD=∠EDA
∴AE=DE ∴AB=DC
∴梯形ABCD是等腰梯形
11、 解：由题意知：（1）PB+PC=8，BC=PC－PB=2
∴PB=2，PC=6
∴PB·PC=(m+2)=12
∴m=10
（2）∴PA2=PB·PC=12
∴PA=
12.解：（1）设规定时间为x天，则
解之，得x
=28，x
=2
经检验可知x=28，x=2都是所列方程的根，但x=2不合题意，舍去，只取x=28
由24＜28知，甲、乙两组合做可在规定时间内完成．
（2）设甲、乙两组合做完成这项工程的
用去了y天，则
解之，得y=20（天）
甲独做剩下工程所需的时间：
（天）
∵20+10=30＞28，∴甲独做剩下的工程不能在规定时间内完成；
乙独做剩下工程所需的时间：
（天）
∵20+6
=26＜28，∴乙独做剩下的工程能在规定时间内完成．
∴我认为抽甲组最好．
13、解答
（1）AO＝BO，DH＝EH，DF＝AF，AC＝DE……3分（少一个扣1分，扣完3分为止）
（2）证明：连EC，AE，
则∠PFC是ΔECF的一个外角，于是∠PFC＝∠ACE＋∠FEC
∵DH⊥AB，AB是⊙O的直径，
∴A是DE中点，即AD=AE，
P C
∴∠AED＝∠ACE ……4分
D
∴∠ACE＋∠FEC＝∠AED＋∠DEC＝∠AEC． F
………………5分
∵PC是⊙O的切线，
A H O B
∴∠PCA＝∠AEC．
∴∠PCA＝∠PFC， E
∴PC＝PF．……………6分
∵PC是切线
∴
，∴
．……7分
（3）在⊙O中，AH
HB＝DHHE＝DH
，
∴
设AF＝，则
．
在
中，
∴
，∴
，即
．
于是
．……9分
由（1）（2）知
，
，解得
．∴
＝
．
∴PC=PF=…10分