二次函数---实践与探索

二次函数---实践与探索(1)　　　　  　班级________姓名________

1.炮弹从炮口射出后，飞行的高度h(m)与飞行时间t(s)之间的函数关系式是h=V₀tsinα－5t²，其中V₀是炮弹发射的初速度，α是炮弹的发射角，当V₀=300（m/s）, α=30˚时,炮弹飞行的最大高度是　　　　 m.

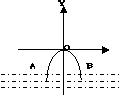
2. .如图，桥拱是抛物线形，其函数解析式为y=－x²,当水位线在AB位置

时,水面宽为12m，这时水面离桥顶的高度h是（　　）

A.3m　 B.2m　　C.4m　　D.9m

4．改革开放以来，某镇通过多种途径发展地方经济，1995年该镇年国民生产总值为2亿元.根据测算，该镇年国民生产总值为5亿元时，可达到小康水平.

（1）若从1996年开始该镇年国民生产总值每年比上一年增加0.6亿元，问该镇经过几年可达到小康水平？

（2）设以2001年为第1年，该镇第x年的年国民生产总值为y亿元，y与x之间的关系是y=－x²+x+5(x≥0).问该镇哪一年的国民生产总值可在1995年的基础上翻两番（即达到1995年的年国民生产总值的4倍）？

5.一合资企业生产某种产品，每件产品成本为3元，售价是4元，年销售量为10万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x（万元）时，产品的年销售量将是原销售量的y倍，且y=－+x+，如果把利润看作是销售总额减去成本费和广告费，试写出年利润S（万元）与广告费x（万元）之间的函数关系式，并计算广告费是多少万元时，公司获得的年利润最大？最大年利润是多少万元？

6．心理学家研究发现一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散，经过实验分析可知，学生的注意力y随时间t的变化规律有如下关系式：

　　　　　 －t²+24t+100　 (0<4≤10)

Y = 　　240　　　　  (10<4≤20)

－7t+380　　　 (20<t≤40)

（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？

（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

（3）一道数学难题，需要讲解24分钟，为了效果好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道难题？

　　　　　　  二次函数---实践与探索(2)

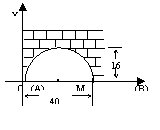
1.　　　 有一拱桥洞抛物线型，这个桥洞的最大高度是16m跨度为40m,现把

它的示意图放在坐标系中，如图26.10.1则抛物线的解析式为(　　)

A.y=－x²+x　 　　　B.y=－x²－x

C.y=－x²+x　　　　 D.y=－x²+x+16　

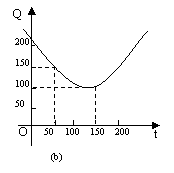
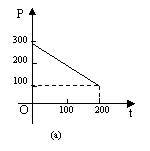
2．.某蔬菜基地种植西红柿，由历年市场行情知，从2月1日起的200天内，西红柿市场售价P与上市时间t的关系用图26.10.4(a)的一条线段表示;西红柿的种植成本Q与上市时间t的关系用图(b)中的抛物线表示,（其中，市场售价和种植成本的单位为：元/100kg, 时间单位为:天）

（1）写出图(a)表示的市场售价P与时间t的函数关系式;

（2）写出图(b)表示的种植成本Q与时间t的函数关系式;

（3）如果市场售价减去种植成本为纯收益，那么何时上市

的西红柿纯收益最大（可借助方程或图像观察）？

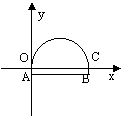3．如图26.10.5所示，有一条双向公路隧道，其横断面由抛物线和矩形ABCO的三边组成，隧道的最大高度为4.9m，AB为10m ，BC为2.4m ,现把隧道的横断面放在平面直角坐标系中. 若有一辆高4m，宽为2m的装有集装箱的汽车要通过隧道，问：如果不考虑其它因素，汽车的右侧离开隧道右壁多少才不至于碰隧道顶部（抛物线部分为隧道顶部，AO、BC为壁）？

 

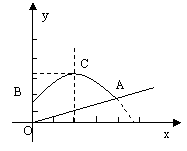4．某农场为防治风沙，在一山坡上种植一片树苗，并安装了自动喷灌设备，一瞬间喷水头喷出的水流呈抛物线，如图所示，建立直角坐标系，已知喷水头B高出地面1.5米，喷水管与山坡所成的夹角∠BOA约为63º，水流最高点C的坐标为（2，3.5）

（1）求此水流抛物线的解析式；

（2）求山坡所在的直线OA的解析式（解析式中的系数精确到0.1）；

（3）计算水喷出后落在山坡上的最远距离OA（精确到0.1米）.