二次函数复习题
一、 填空题(每格2分,共72分)
1、形如 的函数叫做二次函数。此函数的顶点坐标( ),对称轴是 。
2、二次函数![]() 的一般式是
,二次项系数,一次项系数,常数项分别是
。
的一般式是
,二次项系数,一次项系数,常数项分别是
。
3、抛物线![]() 的顶点坐标是
,对称轴是
,开口向_____。
的顶点坐标是
,对称轴是
,开口向_____。
 4、抛物线
4、抛物线![]() 经过点(3,5),则
经过点(3,5),则![]() = ;
= ;
5、抛物线![]() ,若其顶点在
,若其顶点在![]() 轴上,则
轴上,则![]() .
.
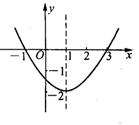
6、抛物线如图所示:当![]() =
时,
=
时,![]() =0,当
=0,当![]() 时,
时,
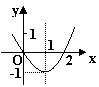
![]() >0;当x
时,
>0;当x
时,![]() <0;
<0;
7、已知二次函数 y=ax2+bx+c 的图像如图所示:则这个二次函数的解析式是 y= 。
8、将抛物线 y=2x2 向下平移 2 个单位,所得的抛物线的解析式为 。
9、函数 y=x2+bx+3 的图象经过点(-1, 0),则 b= 。
10、二次函数 y=(x-1)2+2,∵a , ∴当 x= 时,y 有最 值是 。
11、函数 y=![]() (x-1)2+3,当 x
时,函数值 y 随 x 的增大而增大, 当 x
时,函数值 y 随 x 的增大而减小。
(x-1)2+3,当 x
时,函数值 y 随 x 的增大而增大, 当 x
时,函数值 y 随 x 的增大而减小。
12、将 y=x2-2x+3 化成 y=a (x-m)2+k 的形式,则 y= 。
13、若点 A ( 2, m) 在函数 y=x2-1 的图像上,则 A 点的坐标是 。
14、抛物线 y=2x2+3x-4 与 y 轴的交点坐标是 。
15、请写出一个二次函数以(2, 3)为顶点,且开口向上。 。
16、二次函数![]() , ∵
, ∵![]() _____,∴函数图象与
_____,∴函数图象与![]() 轴有___个交点。
轴有___个交点。
17、用长为2米的铁丝围一个矩形,如果矩形的一边长为x米,面积为y平方米,那么y与x之间的函数关系式 ,自变量的取值范围是 ,面积的最大值 ,此时x的取值为 。
18、与抛物线![]() 关于
关于![]() 轴对称的抛物线的解析式为 。
轴对称的抛物线的解析式为 。
19、抛物线![]() 在
在![]() 轴上截得的线段长度是
。
轴上截得的线段长度是
。
20、二次函数![]() 的值永远为负值的条件是
的值永远为负值的条件是![]() 0,
0,![]() 0。
0。
二、选择题(每题4分,共28分)
21、下列函数中,是二次函数的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
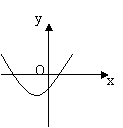 22、二次函数
22、二次函数![]() 图象如图所示,
图象如图所示,
下面结论正确的是( )
A、 ![]() <0,
<0,![]() <0,
<0,![]() >
>![]() B、
B、 ![]() >0,
>0,![]() <0,
<0,![]() >
>![]()
C、![]() >0,
>0,![]() >0,
>0,![]() >
>![]() D、
D、![]() >0,
>0,![]() <0,
<0,![]() <
<![]()
23、满足函数y=x2-4x-4的一个点是( )
A、 (4,4) B、(3,-1) C、(-2,-8) D、![]()
24、把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是( )
 A、 y=3(x+3)2 -2 B、 y=3(x+2)2+2
A、 y=3(x+3)2 -2 B、 y=3(x+2)2+2
C、 y=3(x-3)2 -2 D、 y=3(x-3)2+2
25、某幢建筑物,从10米高的窗口A用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直,(如图)如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是( )
A、 2米 B、 3米 C、 4米 D、 5米
26、函数![]() 经过的象限是( )
经过的象限是( )
A、第一、二、三象限 B、第一、二象限
C、第三、四象限 D、第一、二、四象限
27、二次函数![]() 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
A、![]() =4 B、
=4 B、![]() =3 C、
=3 C、 ![]() =-5
D、
=-5
D、![]() =-1。
=-1。
三、解答题(8+8+10+12+12=50分)
28、(8分)已知抛物线的顶点坐标是(-2,1),且过点(1,-2),求抛物线的解析式。
29、(8分)已知抛物线![]() 的顶点坐标为A,抛物线与x轴的交点为B、C,点B在点C左边,(1)求顶点A的坐标; (2)求点B、C的坐标; (3)求
的顶点坐标为A,抛物线与x轴的交点为B、C,点B在点C左边,(1)求顶点A的坐标; (2)求点B、C的坐标; (3)求![]() ;
;
 30、(12分)如图2-4-20,二次函数的图象与
30、(12分)如图2-4-20,二次函数的图象与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求D点的坐标.(2)求一次函数的解析式.(3)根据图象写出使一次函数值大于二次函数的值的
轴交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求D点的坐标.(2)求一次函数的解析式.(3)根据图象写出使一次函数值大于二次函数的值的![]() 的取值范围.
的取值范围.