九年级上期期末数学模拟测试卷
一、选择题:(每小题2分,共32分)
1.若使分式![]() 的值为零,则x=( )
的值为零,则x=( )
A.2或-2 B.-2 C.2 D.4
2.化简分式![]() 的结果是( )
的结果是( )
A.x2-y2; B.y2-x2; C. x2-4y2; D. 4x2-y2
3.若x2+3x+1=0,则![]() =( )
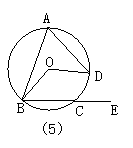
=( )
A.4 B.5 C.6 D.7
4.如果方程4x2-2(m+1)x+m=0 的两个根恰好是一个直角三角形两个锐角的正弦,那么m的值是( )
A.![]() B.
B.![]() C.3;
D.2
C.3;
D.2
5.关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k 的取值范围是( )
A.k≥9 B.k<9; C.k≤9且k≠0 C.k<9且k≠0
6.已知有实数a、b,且知a≠b,又a、b满足着a2=3a+1,b2=3b+1,则a2+ b2之值为( )
A.9 B.10 C.11 D.12
7.已知方程2x2-kx+3=0的一个根是3,那么另一个根是( )
A.![]() B.
B.![]() ;
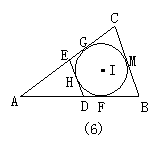
C.-
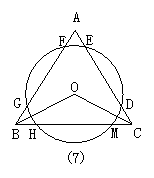
;
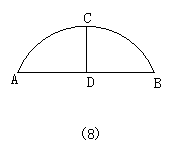
C.-![]() ; D.-
; D.-![]()
8.下列命题中,真命题是( )
A.垂直于半径的直线是圆的切线; B.过三点一定可以作圆
C.优弧一定大于劣弧; D.任意三角形一定有一个外接圆
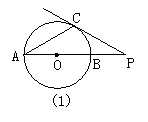
9.如图1所示,已知⊙O的直径AB与弦AC夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为( )
A.![]() ;
B.
;
B.![]() C.10
D.5
C.10
D.5
10.扇形的弧长是20![]() cm,面积是240
cm,面积是240![]() cm2,则扇形的半径是( )
cm2,则扇形的半径是( )
A.24cm B.12cm C.6cm D.28cm
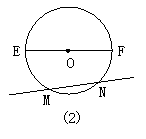
11.如图2所示,EF为⊙O的直径,OE=5cm,弦MN=8cm,那么E、F两点到直线MN的距离之和等于( ) A.12cm B.8cm C.6cm D.3cm
12.已知两圆的半径满足方程x2-![]() +2=0,圆心距为2,则两圆的位置关系为( )
+2=0,圆心距为2,则两圆的位置关系为( )
A.相交 B.外切 C.内切 D.外离
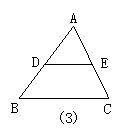
13.如图3所示,D为△ABC的边AB的中点,过D作DE∥BC交AC于E,点F在BC上,使△DEF和△DEA全等,这样的F点的个数有( )
A.4个 B.3个 C.2个 D.1个
14.下列各命题中,假命题是( )
A.全等三角形的对立高相等
B.有两边及第三边上的中线对应相等的两个三角形全等
C.如果一个三角形最大边对的角是锐角, 那么这个三角形一定是锐角三角形
D.所有直角三角形的斜边对应相等
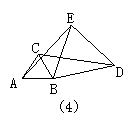
15.如图4所示,△ABC与△BDE都是等边三角形,AB<BD,若△ABC不动,将△BDE绕B点旋转过程中AE与CD的关系为( ) A.AE=CD B.AE>CD C.AE<CD D.无法确定
16.一布袋中有红球8个,白球12个和黄球5个, 它们除了颜色外没有其它区别,闭上眼睛,随机从袋中取出1球不是黄球的概率为( )
A.![]() B.
B.![]() ;
C.
;
C.![]() D.
D.![]()
二、填空题:(每小题2分,共32分)
17.若解分式方程![]() 产生增根,则m=___________.
产生增根,则m=___________.
18.α,β是方程x2+2x-5=0的两个实数根,则α2+αβ+2α的值为_________.
19.已知实数x,y满足(x2+y2)(x2+y2-1)=2,则x2+y2=________.
20.![]() =________.
=________.
21.关于x的方程(m-2)![]() +2x+4=2m-1是一元二次方程,则它的根为_______.
+2x+4=2m-1是一元二次方程,则它的根为_______.
22.已知关于x的方程x2-2x+m=0的一个根是![]() ,则它的另一个根是_____,m= ______.
,则它的另一个根是_____,m= ______.
23.如图5所示,四边形ABCD是⊙O的内接四边形,延长BC到E,已知∠BCD: ∠ECD=3:2,那么 ∠BOD=_______.
24.如图6所示,DE是△ABC的内切圆I的切线,又BC=2cm,△ADE的周长为4cm, 则△ABC的周长是______cm.
25.在△ABC中,∠A=70°,⊙O在△ABC的三边上截得的三条弦都相等, 如图7所示,则∠BOC=________度.
26.如图8所示,已知有一圆形桥拱,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是________cm.
27.△ABC中,∠C=90°,∠A=30°,AC=3,则它的内切圆直径为______.
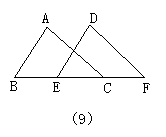
28.如图9所示,在△ABC与△DEF中,如果AB=DE,BC=EF,只要再找出∠_____=∠______或______=_____,就可证明这两个三角形全等.
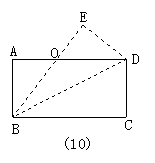
29.已知如图10所示,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段___________(不包括AB=CD和AD=BC).
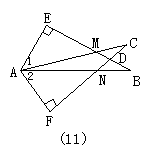
30.如图11所示,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2; ②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是________.
31.为了了解我国15岁男孩的平均身高,从北方抽取了300个男孩,平均身高是1.6m;从南方抽取了200个男孩,平均身高为1.50m,又若:我国北方男孩数与南方男孩数的比值为3:2,由此可推断(估计)我国15岁男孩的平均身高,现有4个大约结果:①1.54m,②1.55m,③1.56m,④1.57m,你认为结果应该是_______.
32.为了估计池塘里有多少条鱼,从池塘里捕捉了100条鱼,做上标记, 然后放回池塘里,经过一段时间后,等有标记的鱼完全混合于池塘中鱼群后, 再捕第二次样本鱼200条,发现其中有标志的鱼25条,你估计一下,该池塘里现在有鱼____条.
三、解答题:
33. (5分)解方程:![]() .
.
34. (5分)先化简再求值:![]() , 其中a=3.
, 其中a=3.
35. (5分)解方程:3(x-5)2=2(5-x).
36. (5分)已知一元二次方程kx2+x+1=0
(1)当它有两个实数根时,求k的取值范围;
(2)问:k为何值时,原方程的两实数根的平方和为3?
37.(8分)某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施. 经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平场每天的盈利最多,请你为商场设计降价方案.
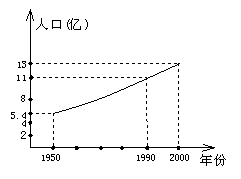
38.(6分)新中国成立后,社会安定,我国人口数量逐年增加, 人均资源不足的矛盾日益突出,为实施可持续性发展战略,我国把实行计划生育作为一项基本国策,下图是我国人口增长图,试根据图象信息,回答下列问题:
(1)1950年到1990年我国人口增加了_____亿,2000年我国人口数量为_____亿.
(2)实行计划生育政策前我国人口平均每五年增长10%, 由于实行了计划生育,我国从1990年到2000年这十年间就少出生了______亿人.
(3)如图所示,1990年2000年这十年间,我国人口平均每五年的增长率约是多少?
 |
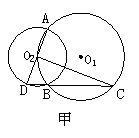
39. (6分)已知⊙O1与⊙O2相交于A、B两点,且点O2在⊙O1上.
(1)如图甲所示,AD是⊙O2的直径,连DB并延长交⊙O1于C,求证:CO2⊥AD.
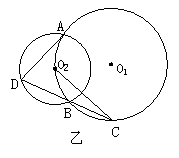
(2)如图乙所示,如果AD是⊙O2的一条弦,连DB并延长交⊙O1于C,那么CO2所在的直线是否与AD垂直?证明你的结论.
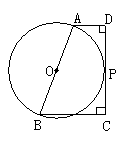
40. (8分)如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB 为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.
求证:(1)PC、PD是关于x的方程:x2-ax+mn=0的两根;
(2)a2=4mn.
答案:
一、1.B 2.A 3.D 4.B 5.D 6.C 7.A 8.D
9.A 解:连结OC,∵PC是⊙O的切线,∴OC⊥PC,∵∠A=30°,OA=OC,
∴∠OCA=∠A=30°, ∴∠COP=60°,在Rt△OCP中,tan∠COP=![]() ,
,
∴OC=![]() .
.
点拨:此题运用切线的性质及三角函数的意义来解决.
10.A 解:∵S扇形=![]() LR,S扇形=240
LR,S扇形=240![]() ,L=20
,L=20![]() ,
,
∴240![]() =
=![]() ×20
×20![]() ×R, ∴R=24(cm)
×R, ∴R=24(cm)
点拨:此题要正确使用扇形的面积公式来进行解决, 在计算时避免将“”取近似值3.14.
11.C 解:作EA⊥MN,FB⊥MN,OH⊥MN,垂足分别为A、B、H,则EA∥OH∥FB.
∵OE=OF,∴HA=HB,∴OH是梯形EABF的中位线,∴OH=![]() (EA+BF),∴EA+BF= 2OH.
(EA+BF),∴EA+BF= 2OH.
∵OE=OM=5(cm),弦MN=8cm,∴MN=4cm,∴OH=![]() =3,∴EA+BF=2×3=6(cm).
=3,∴EA+BF=2×3=6(cm).
点拨:在进行与圆有关的计算时,常常过圆心作弦的垂线段, 再运用垂径定理、勾股定理等知识来解决使题目化难为易.
12.A 解:设R,r是方程x2-![]() +2=0的两根(R>r),
+2=0的两根(R>r),
∴R+r=![]() ,Rr=2,
,Rr=2,
∴R-r=![]()
又∵d=2,∴0<d<![]() ,即R-r<d<R+r.
,即R-r<d<R+r.
点拨:此题从数量关系方面判别圆与圆的位置关系,应加强其解题思路的训练.
13.D 解:取BC的中点F,连结FD、FE,∵D、E是AB、AC中点,F 是BC中点,
∴DF∥AC,EF∥AB.
∴四边形AEFD是平行四边形.
∴△AED≌△FDE,故在BC上的点F的个数有1个.
点拨:此题是对两三角形的全等及三角形的中位线定理的综合应用,应加强解题思路与方法的应用训练.
14.D 解:∵直角三角形的斜边不一定相等,∴D是假命题.
点拨:此题是对命题真假的判定的应用,应熟练地判定命题的真假, 提高分析判别能力.
15.A 解: ∵△ABC与△BDE是等边三角形,∴BA=BC,BE=BD,∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,即∠ABE=∠CBD,∴△ABE≌△CBD,∴AE=CD.
点拨:此题应用两三角形全等的识别法来解决,应熟练应用这种解题思路.
16.A 解:∵从袋中取出1球,不是黄球的概率为![]() .
.
点拨:此题是对概率知识的应用,应明确概率的实质并能具体地应用.
二、
17.m=-2或m=1
解:∵![]() ,∴2x2-(m+1)=(x+1)2,2x2-m-1=x2+2x+1,x2-2x-m-2=0,
,∴2x2-(m+1)=(x+1)2,2x2-m-1=x2+2x+1,x2-2x-m-2=0,
欲使原方程有增根,需x=0或x=-1,当x=0时,02-2×0-m-2=0,
∴m=-2,当x=-1时,(-1)2-2×(-1)-m-2=0,∴m=1,故m=-2或m=1.
点拨:此题运用方程增根的意义使问题得以解决,这种方法经常使用, 应要熟练掌握.
18.0
点拨:此题运用一元二次方程根与系数关系及方程根的意义来解决,容易忽视方程根的意义,而将所求的代数式强加变型,使式子更加复杂,难以得出a2+2a=5.
19.2 解:∵(x2+y2)(x2+y2-1)=2,∴(x2+y2)2-(x2+y2)-2=0,∴(x2+y2-2)(x2+y2+1)=0,
∴x2+y2=2或x2+y2=-1,∵x2+y2=-1(舍去),故x2+y2=2,
点拨: 此题应用换元法,将x2+y2≥0,而将其负值也取上的错误.
20.-ab12 解:(-a2b3)2·(-b2a-1)3=a4b6·(-b6a-3)=-ab12.
点拨:此题运用幂的运算性质来进行化简.应记牢运算原则,正确地进行计算化简,确保运算的正确性.
21. ![]() .
.
解:欲使方程(m-2)![]() +2x+4=2m-1是一元二次方程,须
+2x+4=2m-1是一元二次方程,须![]() ,
,
∴m=-2,当m=-2时, 原方程为:-4x2+2x+4=-4-1,∴4x2-2x-9=0,x=![]() .
.
点拨:此题根据一元二次方程的意义确定特定系数m的值之后, 再根据公式法求方程的根,不要忽视二次项系数不等于零的条件限制.
22.另一个根1-![]() ,m=-2.
,m=-2.
解:设x2-2x+m=0的另一个根为x1,则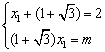 ,∴
,∴![]()
点拨:此题是一元二次方程根与系数之间关系的综合应用,本题也可由方程根的意义来解决.
23.144° 解:∵∠BCD:∠ECD=3:2, 设∠BCD=3k,则∠ECD=2k,
∵∠BCD+∠ECD=180°,∴3k+2k=180°,∴k=36°,∴∠BCD=108°,∠ECD=72°,
∴∠A= 72°,∴∠BOD=144°.
点拨:此题由圆的有关性质及圆周角性质来解决,易将圆周角性质与圆心角性质发生混淆.
24.8 解:∵⊙I与EC、ED、BC、BD分别相切于G、H、M、F,
∴ EG=EH,DH=DF,BF=BM,CG=CM,∴EG+DF=EH+DH=DE,CG+BF=CM+BM=BC,
∵BC=2,AD+AE+DE=4,
∴△ABC的周长为AD+AE+(EG+DF)+(CG+BF)+BC=(AD+AE+DE)+BC+BC=4+2+2=8.
点拨:此题运用切线长定理来进行解决,这种等量代换及解题方法是非常重要的,应切实掌握.
25.125° 解:作OL⊥AB、OQ⊥BC、ON⊥AC,垂足分别为L、Q、N.
∵FG=HM=DE,∴OL=OQ=ON,∴O是△ABC的内心,
∵∠A=70°,∴∠OBC+∠OCB=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-70°)=55°,
(180°-70°)=55°,
∴∠BOC=180°-55°=125°.
点拨:此题是用圆的有关性质及内心的意义来解决,应特别注重辅助线的添置.
26.10 解:设O为拱形所在圆的圆心,作半径OC⊥AB,垂足为D, 连结OA,
设拱形所在圆的半径为
cm,则OA=x,OD=x-4,AD=![]() AB=
AB=![]() ×16=8,
×16=8,
在Rt△OAD中,由勾股定理得OA2=AD2+OD2,∴x2=82+(x-4)2,解得x=10(cm).
点拨:此题是垂径定理及勾股定理的综合应用,应明确这种作辅助线的方法及解题思路.
27. ![]() 解:∵∠A=30°,AC=3,cosA=
解:∵∠A=30°,AC=3,cosA=![]() ,∴ AB=
,∴ AB=![]()
∵BC=![]() AB=
AB=![]()
∴其内切圆直径d=2 ×![]() (AC+BC-AB)=
(AC+BC-AB)=![]() .
.
点拨:此题是三角函数与直角三角形内切圆半径公式的综合应用.
28.∠ABC=∠DEF或AC=DF.
解:在△ABC和△DEF中,∵AB=DE,BC=EF,∴若∠ABC=∠DEF, 则△ABC≌△DEF,
△ABC和△DEF中,∵AB=DE,BC=EF,∴若AC=BF,则△ABC≌△DEF.
点拨:此题是对两三角形全等识别法的考查,应加强两三角形全等识别法的理解与应用.
29.OB=OD 解: ∵△BDE是由△BDC沿BD对折而得,∴△BED≌△BCD,∴∠EBD=∠CBD,
∵矩形ABCD,∴AD∥BC,∴∠ODB=∠CBD,∴∠OBD=∠ODB,∴OB=OD.
点拨:此题是将三角形沿某直线对折的应用.易忽视△BED≌△BCD.
30.①∠1=∠2;②BE=CF;③△ACN≌△ABM.
解:如答图所示,在△ABE和△ACF中,∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE ≌△ACF,∴AB=AC,BE=CF,∠EAB=∠FAC,∴∠EAB-∠CAN=∠FAC-∠CAN,
∴∠1=∠2.在△ACN和△ABM中,AC=AB,∠C=∠B,∠CAN=∠BAM,∴△ACN≌△ABM.
点拨:此题是两三角形全等的识别法及特征的综合应用.
31.③ 解:我国15岁男孩的平均身高为: ![]() =1.55(m)
=1.55(m)
点拨:此题考查的内容是用样本特征估计总体的特征,应明确, 在用样本去估计总体时所选取的样本要具有代表性.
32. 800条 解:设该池塘里现有鱼x条,由题意知![]() ,∴x=800条.
,∴x=800条.
点拨:此题是用样本估计总体的具体应用,在选取样本时一定要使样本足够大, 以提高估计的真实性.
三、
33.解: ![]() ,去分母化为3(x-2)+4(x+2)=16,3x-6+4x+8-16=0,7x-14=0,
,去分母化为3(x-2)+4(x+2)=16,3x-6+4x+8-16=0,7x-14=0,
∴x=2, 经检验x=2是原方程的增根,∴原方程无解.
点拨:此题是解分式方程的应用,易忘记验根.
34. ![]() .
.
点拨:此题先对分式化简计算再求值.
35.
x=5或x=![]()
解:整理:3(x-5)2-2(5-x)=0,
3(x-5)2+2(x-5)=0,(x-5)[3(x-5) +2]=0,(x-5)(3x-13)=0,x-5=0或3x-13=0,
∴x=5或x=![]() .
.
点拨:此题用因式分解法来解一元二次方程,不需化成一般形式再应用求根公式解决.
36.
解:(1)由题意得![]() ,
,![]() .
.
(2) ∵ x12+x22=3, ∴(x1+x2)2-2x1x2=3,
∵x1+x2=![]() , x1x2=
, x1x2=![]() ,
,
∴![]()
∴k1=![]() ,k2=-1
,k2=-1
∵![]()
∴k=-1.
点拨:此题是一元二次方程根与系数的关系及方程根的判别式的综合应用,易错点有:①难以考虑到将方程![]() 经过整理看作
经过整理看作![]() 的一元二次方程,②求得k值后忘记检验是否符合题意.
的一元二次方程,②求得k值后忘记检验是否符合题意.
37.解:(1)设每件衬衣应降低x元,由题意得(40-x)(20+2x)=1200,∴x1= 10,x2=20,
∵为了扩大销售,增加盈利,尽快减少库存,∴x=20.
(2) 设每件衬衣应降低x元,由题意得商场平均每天的盈利为
(40-x)(20+2x)=-2x2+60x+800=-2(x-15)2+ 1250,∴当x=15时,平均每天盈利的最大值为1250元.
点拨:此题是新型应用题的解法,应明确其解题思路、方法;在解(1)中应理解“增加盈利,减少库存”的实际含义,这道数学应用题颇有新意,在市场经济大潮中,一方面商家追求最大利润,而另一方面买家却渴望费用最小,这也就是近年来与经济生活有关的最值型应用题日趋增多的原因.
38.(1)5.6;13 (2)0.31 (3)8.7%
解:设1990年到2000年这十年间, 我国人口平均每五年的增长率是x,由图象知11(x+2)2=13,(1+x)2=![]() ,∴1+x=±1.087,∴x1 ≈8.7%,x2≈-2.087(舍去).
,∴1+x=±1.087,∴x1 ≈8.7%,x2≈-2.087(舍去).
点拨:这是一道利用图象解决实际问题的典型题目,要特别注意图像所提供的信息,要善于从图像上找答案.
39.(1)证明:连结AB, ∵AD是⊙O2的直径,∴∠ABD=90°,∴∠D+∠DAB=90°,
又∵∠DAB=∠DCO2,∴∠D+∠DCO2=90°,∴∠DO2C=90°,即CO2 ⊥AD.
(2)证明:过A作⊙O2的直径AD′,连结D′B、AB,设直径CO2 交AD于E,
∵AD′是⊙O2的直径,∴∠ABD′=90°,∴∠D′+∠D′AB=90°,
∵∠D=∠D′, ∠D′AB=∠DCE,∴∠D+∠DCE=90°,∴∠DEC=90°,即直线CO2⊥AD.
点拨:此题是与圆有关性质的综合应用,由直径挖掘出直角已成为规律.
40. (1)连结OP.∵CD切⊙O于P,∴OP⊥CD,
∵AD⊥CD,BC⊥CD,∴AD∥OP∥BC.
又∵OA=OB,∴PC=PD,
∵CD=a,∴PC+PD=CD=a,
连结PA、PB,∵AB是⊙O 的直径,∴∠APB=90°,∴∠APD+∠BPC=90°,
∵∠D=90°,∴∠APD+∠PAD=90°,∴∠PAD=∠BPC,
又∵∠D=∠C=90°,∴△PAD∽△BPC,
∴![]() ,∴PD·PC=AD·BC.
,∴PD·PC=AD·BC.
∵AD=m,BC= n,∴PD·PC=m·n,
故PC、PD是关于x的方程x2-ax+mn=0的两根.
(2)∵CD=PD+PC,PD=PC,CD=a,∴PC=![]() ,∴PC2=
,∴PC2=![]() ,又PC2=PC·PD,PD·PC=m·n,
,又PC2=PC·PD,PD·PC=m·n,
∴ ![]() =mn,∴a2=4mn.
=mn,∴a2=4mn.
点拨:此题是学科内综合题,是一元二次方程,两三角形相似的识别法,切线的性质及与圆有关的性质的综合应用,通过本题加深了这些知识的联系和沟通,提高了应用能力.