九年级上数学二次函数测试卷

九年级上数学《二次函数》单元测试卷

姓名______________

一、选择题（共30分）

 1．二次函数y=x²+4x+c的对称轴方程是 　　　　　　　　 （　　）

　　　 A.x = -2　　　 B.x=1　　　C.x=2　　　 D.由c的值确定

2．已知抛物线y=ax²+bx+c经过原点和第一、二、三象限，那么(　　 )

 A.a>0,b>0,c>0　　B.a<0,b<0,c=0　 C.a<0,b<0,c>0　　D.a>0,b>0,c=0

3．若（2, 5）、（4, 5）是抛物线y = ax²+bx+c上的两点，则它的对称轴方程是 (　　 )

　 A.x = -1　　　　 B.x = 1　　  C.x = 2　　　 D.x = 3

4．若直线y=x-n与抛物线y = x²-x-n的交点在x轴上，则n的取值一定为　 （　　）

A.0　　　　 B.2　　　　  C.0或2　　　D.任意实数

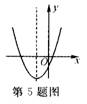
5．二次函数y = ax²+bx+c的图像如图所示，则点（）

在直角坐标系中的　　　　　　　　　　　　 （　 ）

　A．第一象限　　　　  B．第二象限　　　　

C．第三象限　　　　  D．第四象限

6.抛物线y=x²-8x+c的顶点在x轴上，则c等于(　　)

A.-16　　 B.-4　　　　C.8　　　　　　 D.16

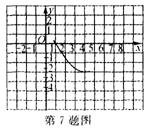
7．已知抛物线y=的部分图像(如图)图像再次与x　

轴相交时的坐标是　　　　　　　 　　　　　　　 (　　)

A.(5,0)　　　  B.(6,0 )　　　  C.(7,0)　　　 D.(8,0 )

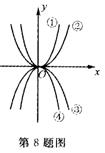
8．如图，四个二次函数的图像中，分别对应的是①y = ax²；②y = ax²；

③y = cx²； ④y = cx²．则a、b、c、d的大小关系为（　　）

A.a>b>c>d　　 B. a>b>d> c　　 C.b > a >c>d　　D.b>a>d> c

9.已知抛物线y=-x²+mx+n的顶点坐标是（-1，- 3 )，

则m和n的值分别是（　　）

 

 A.2,4　　　　  B.-2,-4　　 C.2,-4　　　　 D.-2,0

10.抛物线y=x²-(m+2)x+3(m-1)与x轴　　　　　　　 （　　）

　A.一定有两个交点　　　　　　　　　　　 B．只有一个交点

C．有两个或一个交点　　　　　　　　　  D．没有交点

二、填空题（共24分）

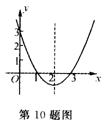　　11.抛物线y = ax²+bx+c如图所示，则它关于x轴对称的抛物线的

　　　 解析式是　　　　　  .

　　12.若抛物线y = x²+(k-1)x+(k+3)经过原点，则k=　　　.

　　13.如果函数y = ax²+4x-的图像的顶点的横坐标为l，则a的值为　　.

　　14.已知抛物线y = ax²+12x-19的顶点的横坐标是3，则 a=　　　 .

　　15.抛物线y = a(x-k)²+m的对称轴是直线　　　 ，顶点坐标是　　  .

16.抛物线y = 2x²+bx+c的顶点坐标为（2，-3)，则b=　　  , c=　　  .

三、解答题（共 46分）

17.(8分）把抛物线y=ax²+bx+c向左平移2个单位，同时向下平移l个单位后，恰好与抛物线y=2x²+4x+1重合．请求出a、b、c的值，并画出一个比较准确的示意图．

 18.(8分）已知二次函数的图像经过（3,0）、（2，-3）点，对称轴x=l，求这个函数的解析式．

　　

19.(12分）已知函数y = x²+bx-1的图像经过（3,2).

 (l）求这个函数的解析式； (2）画出它的图像，并指出图像的顶点坐标；

(3）当x>0时，求使y2的x的取值范围．

　　

20.(8分）已知抛物线的顶点坐标为M(l,-2 )，且经过点N(2,3)．求此二次函数的解析式．

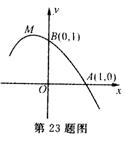21.(10分）二次函数y=ax²+bx+c的图像的一部分如下图，已知它的顶点M在第二象限，且该函数图像经过点A (l,0）和点B(0,1).

　 (1）请判断实数a的取值范围，并说明理由；

(2）设此二次函数的图像与x轴的另一个交点为c，当△AMC的面积为△ABC面积的1.25倍时，求a的值．