九 年 级 上 数 学 综 合 测 试 卷
班级 姓名 成绩 2006.10.
一、选择题：（每小题2分，共20分）
1、小明从正面观察下图所示的两个物体，看到的是 （ ）
2、关于
的方程
是一元二次方程的条件是（ ）
A、
B、
C、且 D、
3、用配方法解一元二次方程
则方程可变形为（ ）
A、
B、
C、
D、
4、下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A、平行四边形、菱形、正方形 B、等腰梯形、矩形、正方形
C、 等边三角形、矩形、圆 D、菱形、正方形、圆
5、下列性质中，正方形具有而菱形不一定具有的是（ ）
A、对角线相等 B、对角线互相平分
C、对角线互相垂直 D、每条对角线平分一组对角
6、△ABC中，
，那么△ABC是（ ）
A、等腰三角形但不是直角三角形
B、直角三角形但不是等腰三角形
C、等腰直角三角形
D、含30°角的直角三角形
7、下列说法不正确的是（ ）
A、顺次连接任意四边形的各边中点都可得到平行四边形
B、对角线互相垂直的矩形是正方形
C、顺次连接等腰梯形的各边中点得到的是矩形
D、三角形的三内角平分线交于一点且到三边的距离相等
8、在Rt△ABC中，∠ACB=90°，∠A=30°，AC=
㎝，则AB边上的中线是( )
A、1㎝ B、2㎝ C、1.5㎝ D、
㎝
9、已知x=1是二次方程(m2-1)x2-mx+m2=0的一个根,那么m的值是( )
A、
B、
C、
D、
10、制造一种产品，原来每件成本是200元，由于连续两次降低成本，现在的成本是162元，则平均每次降低成本（ ）
A、8．5％ B、9％ C9、．5％ D、10％
二、填空题（每小题3分，共18分）
11、方程
，化成一般形式是
，其二次项的系数和一次项系数的和是 ，它的解是
；
12、x2=2x 的根是 ，x2-8=0的根是 ，2（x-1）2=4的根是 ；
13、矩形的两条对角线的一个夹角是60°，两条对角线的和是8cm，则矩形的较短边长
是 cm，周长是 cm，较长边与对角线的夹角是 ；
14、一张桌子摆放若干碟子，从三个方向上看，三种视图如图所示，则这张桌子上共有 个碟子；
15、如图，以正方形ABCD的边BC为边向形内作等边△PBC，连接AP、DP，则∠ABP= ， ∠APB= ，若AB=2cm，则S△ABP= ；
16、等腰梯形的上、下底分别为6
、8，且有一个角为60°，则它的腰为___________；
三、用适当的方法解下列方程（每题5分，共20分）
17、2x2－4x－1=0; 18、x－2=x(x－2);
19、(x－2)(x－3)=12;
20、
;
四、解答题（第21、22、23题每题6分，第24题10分，第25题14分，共42分）
21、(6分)画下面几何体的三视图
 |
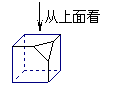22、（6分）某西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克，为了促销，该经营户决定降价销售。经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克。另外，每天的房租等固定成本共24元。该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？
23、（6分）已知：E、F是四边形ABCD的对角线AC上的两点，AF=CE，四边形DEBF是平行四边形。求证：四边形ABCD是平行四边形。
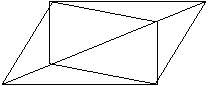D
C
F
E
A B
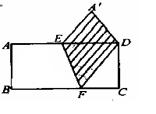24、（10分）如图：把一个矩形如图折叠，使顶点B和D重合，折痕为EF。（1）找出全等三角形(不能添加辅助线)；（2）判断△DEF的形状,并证明；（3）连接BE，判断四边形BEDF的形状，并证明。
25、（14分）如图①，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE。(不需要证明)
(1)如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF。则上面的结论①、②是否仍然成立？(请直接回答“成立”或“不成立”)
(2)如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由。
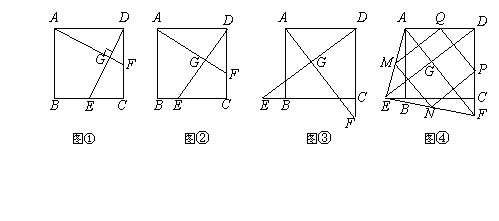(3)如图④，在(2)的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程。