初三数学测验卷(总分120)
班级： 姓名： 成绩：
一、填空题（每小题3分，共30分）
1. 在四边形ABCD中，AB∥DC，AD∥BC，如果∠B=50°，那么∠D=________.
2．在Rt
中，
，点
是斜边
的中点，
，则
．
3．已知菱形
的边长
cm，对角线
cm，则菱形的面积=
．
4．如图，在中，
平分
，
，则点到的距离为_________．
 |
第4题图 第7题图 第8题图
5．方程
的根是
．
6．已知一个一元二次方程的两根满足 ①
, ②
,请写出一个符合条件的一元二次方程:_________________________．
7．如图，为了求出湖两岸A、B两点间的距离，观测者从测点A、B分别测得∠BAC＝
°，
∠ABC＝
°，又量得BC＝
，则A、B两点间的距离为 （结果保留根号）．
8．如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______．
9.某市教育经费从2003年的8千万元增加到2005年的9.68千万元，则这两年的教育经费平均增长率是____________.
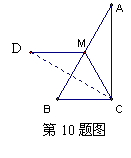
10.如图, 在RtΔABC,∠ACB=900,∠A<∠B，CM是斜边AB的中线，
将ΔACM沿直线CM折叠，点A落在点D处，若CD恰好与AB
垂直，则∠A等于 度．
二、选择题（每小题3分，共24分）
11.下列方程是一元二次方程的是-------------------------------------------------------------------（ ）
A． 
B． 
C．
D． 
12.下列条件中不能用来判断平行四边形的是---------------------------------------------------（ ）
A．两组对边互相平行 B．两组对边相等
C．一组对边平行且相等 D．一组对边相等，另一组对边平行
13. 用配方法解方程
，变形后的形式为------------------------------------（ ）A.
B.
C.
D.
14. 到△ABC的三个顶点距离相等的点是△ABC的-------------------------------------------（ ）
A. 三条中线的交点 B. 三条角平分线的交点
C. 三条高线的交点 D. 三条边的垂直平分线的交点
15. 三角形两边长分别为3和6，第三边是一元二次方程
的解，则这
个三角形的周长是--------------------------------------------------------------------------------- ( )
A.11 B.13 C.11或13 D.11和13
16.下列矩形中，按虚线剪开后，既能拼出四边形和梯形，又能拼出三角形的是-------（ ）
17．如图，E、F、G、H分别是四边形ABCD四条边的中点，要
使四边形EFGH为菱形，四边形ABCD应具备的条件是-----（ ）
A．
B．
C．
D．
第17题
18．关于x的一元二次方程（a－1）x2＋x+a2－l=0的一个根是0.则a的值为-------------------( )
A、1
B、-l C、1 或－1 D、
三、解方程（每小题5分，共20分）
19. 
20. 
21. 
22. 
四、解答题
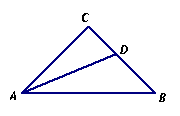
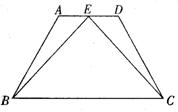23. (7分) 已知：如图，四边形ABCD是等腰梯形，AB＝DC，AD∥BC，点E在AD上，
且EB＝EC，试问点E是AD的中点吗？若是，请给出证明，若不是，请说明理由．
24. (7分) 已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，
且EA⊥AF.
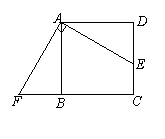求证：DE=BF.
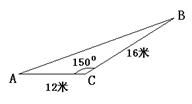25. (7分) 如图，一居民生活小区内有一块三角形空地ABC，AC=12米，BC=16米，∠C=1500，为了美化环境，决定在这块空地种植花草，预计每平方米投入绿化资金20元，求共需要多少资金？
26．(8分) 有一农户用24米长的篱笆围成一面靠墙(墙长为12米),大小相等且彼此相连的三个矩形鸡舍,(如图所示)鸡场的面积能够达到32米2吗?若能,给出你的方案?若不能,请说明理由．
27. (8分) 某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯每上涨1元，其销售量将减少10个。为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？
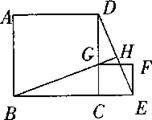
28. (9分) 如图，正方形ABCD的边长为1，G为CD边上的一个动点（G与C、D不重合），以CG为一边向正方形ABCD做外正方形GCEF，连接DE交BG的延长线于H。
（1）求证：①△BCG≌△DCE；②BH⊥DE；
（2）当G点运动到什么位置时，BH垂直平分DE？请说明理由。
