2006—2007学年度第一学期九年级第一次月考
数学试题
班级： 姓名： 座号： 得分：
说明：考试时间90分钟，总分100分
| 题号 | 一 | 二 | 三 | 总分 |
| 得分 |
一、选择题（每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 |
1、在⊿ABC所在的平面内存在一点P，它到A、B、C三点的距离都相等，那么点P一定是：
A、⊿ABC三边中垂线的交点 B、⊿ABC三边上高线的交点
C、⊿ABC三内角平分线的交点 D、⊿ABC一条中位线的中点
2、已知等腰三角形的一个底角等于30°，则这个等腰三角形的顶角等于:
A.150° B.120° C.75° D.30°
3、关于x的方程ax2–3x+2=0是一元二次方程，则:
A．a＞0 B．a≠0 C．a＝1 D．a≥0
4、方程x2+6x–5=0的左边配成完全平方后所得方程为:
A.(x+3)2=14 B.(x–3)2=14 C.(x+3)2=4 D. (x–3)2=4
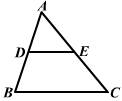
5、如图，在△ABC中，D、E分别是AB、AC边的中点，且AB=10，AC=14，BC=16，
则DE等于:
A．5 B．7 C．8 D．12
6、在△ABC中，∠A＝50°，AB＝AC，AB的垂直平分线DE交AC于D，则∠DBC的度数是:
A.20° B.15° C.30° D.25°
7、方程x2 = 2x的解是:
A、x=2
B、x1=
，x2= 0 C、x1=2，x2=0 D、x = 0
8、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年（2001年～2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的增长率都是x，那么x满足的方程为:
A、(1+x)2=2 B、(1+x)2=4 C、1+2x=2 D、(1+x)+2(1+x)=4
9、关于x的一元二次方程（a－1）x2＋x+a2－l=0的一个根是0.则a的值为:
A、1
B、-l C、1 或－1 D、
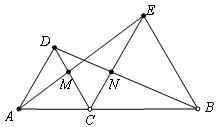
10、如图，△DAC和△EBC均是等边三角形，AE、BD分别与
CD、CE交于点M、N，有如下结论：
① △ACE≌△DCB； ② CM＝CN；③ AC＝DN。其中，
正确结论的个数是:
(A) 3个 （B）2个
(C) 1个 （D）0个
二、填空题（每小题3分，共15分）
11、方程(x＋1)(x－2)＝0的根是 ．
12、Rt⊿ABC中，∠C=90º，∠B=30º，则AB边上的中线与AC的关系是 。
13、已知m是方程x2-x-2=0的一个根，则代数式m2-m的值是 。
14、如图，若将四根木条钉成的矩形木框变为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 。
 | |||
 | |||
第14题 第15题
15、如图，为了求出湖两岸A、B两点间的距离，观测者从测点A、B分别测得∠BAC＝90°，∠ABC＝30°，又量得BC＝160 m，则A、B两点间的距离为 m（结果保留根号）
三、解答题（55分）
16、（6分）用配方法解关于x的一元二次方程：ax2+bx+c=0（其中a≠0）
17、关于x的一元二次方程mx2- (3m-1)x+2m-1=0 , 其根的判别式的值为1，求m的值及该方程的根。（7分）
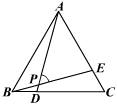
18、（8分）如图，等边△ABC中，BD=CE，AD与BE相交于点P，求∠APE的度数。
19、（8分）为了把一个长100m宽60m 的游泳池扩建成一个周长为600 m的大型水上游乐场，把游泳池的长增加x m，那么x等于多少时，水上游乐场的面积为20000㎡？如果能，求出x的值；如果不能，请说明理由。
20、（8分）某服装店平均每天售出“贝贝”牌童装20件, 每件获利30元,为了迎接“六一”儿童节,商场决定适当降价,经过市场调查发现：如果每件童装每降价4元,那么平均每天就可多售出8件,要想平均每天获利800元,每件童装应降价多少元?
21、（8分）已知：如图，在□ABCD 中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．
（1）求证：△ADE≌△CBF；
（2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．
 |
22、（10分）如图22－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
（1）如图22－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
（2）若三角尺GEF旋转到如图22－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．
 |