华师大九年级（上）期末大复习
第Ⅰ卷（满分48分）
一、选择题：（每小题3分，共48分）
1、下列条件中，不一定能使两个三角形全等的条件是（ ）
（A）两边一角对应相等 （B）两角一边对应相等
（C）三边对应相等 （D）两边和它们的夹角对应相等
2、计算：
的结果是（ ）
A、m+2
B、m－2 C、
D、
3、方程(a+2)a+3ax+1=0是关于x的一元二次方程，则a的值为（ ）
A、a =±2 B、a=2 C、a=－2 D、a≠－2
4、若x＜2，则
的值为（ ）
A、－1 B、0 C、1 D、2
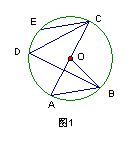5、如图1，AC是⊙O的直径，BD是⊙O的弦，EC∥AB交⊙O于E，则图中与
∠BOC相等的角共有（ ）
A、2个 B、3个 C、4个 D、5个
6、如果关于x的一元二次方程Kx2－6x+9=0有两个不相等的实数根，那么K的取值范围是（ ）
A、K＜1 B、K≠0 C、K＜1且K≠0 D、K＞1
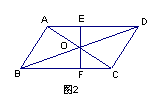7、如图2，O为
ABCD的对角线AC、BD的交点，过O的直线与边AD、BC分别交于点E、F，则图中全等的三角形共有（ ）
A、2对 B、3对 C、5对 D、6对
8、圆心都在x轴上的两圆有一个公共点是（1，2），那么这两圆的关系是（ ）
A、内切 B、外切 C、相交 D、外离
9、如果圆锥的底面半径为3cm，母线长为4cm，那么它的侧面积等于（ ）
A、24
cm2 B、12cm2 C、12cm2 D、6cm2
10、下面是赵明同学在一次测验中解答的填空题，其中，正确的是（ ）
A、若x2 =4，则x=2
B、方程x(2x－1)=2x－1的解为x =1
C、关于x的方程x2－3x +m=0的一个根是1, 那么m = 2
D、若分式
的值为零，则x = 1或x = 2
11、下列命题中，真命题是（ ）
A、有两边相等的平行四边形是菱形。
B、有一个角是直角的四边形是矩形。
C、直径是圆中最长的弦。
D、三点确定一个圆。
12、下列命题中，假命题是（ ）
A、两个三角形全等，则它们的周长相等。
B、成轴对称的两个三角形全等。
C、底边和顶角对应相等的两个等腰三角形全等。
D、有一边和一个角对应相等的两个三角形全等。
13、如图3，AB是半圆O的直径，弦AD、BC相交于P，那么
等于（ ）
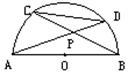A、sin∠BPD B、cos∠BPD
C、tan∠BPD D、cot∠BPD 图3
14、已知两圆的半径分别为5cm和7cm，当两圆
相离时，它们的圆心距d的大小应满足（ ）
A、d＞2 B、d＜2 C、2＜d＜12 D 、d＜2或 d＞12
15、一项工程，甲需6天完成，乙需4天完成，求两人合作完成需要的天数。如果设两人合作需要x天完成，则所列方程正确的是（ ）
A、6+4=2x B、
C、
D、x=6+4
16、抛掷一枚普通的硬币，连续出现三个正面的概率是（ ）
A、 B、
C、
D、
第Ⅱ卷
二、填空题：（每小题3分，共18分）
1、一种细菌的半径为0.00004m，用科学记数法把它表示为____________m
2、计算：（－2xy2）2·3x2y÷(－x3y4) =____________。
3、为了了解一批灯泡的使用寿命，适合采用__________调查方式。
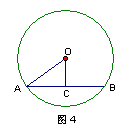
4、如图4，在⊙O中，AB为弦，OC⊥AB，垂足为C，若AO=5cm,OC=3cm，则弦AB的长为_______cm。
5、若
，则
=_______。
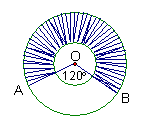
6、如图5，在同心圆中，两圆的半径分别为20cm和
10cm，∠AOB=120°。则图中阴影部分的面积为
_______ 图5
三、（每小题6分，共12分）
1、计算：
2、先化简，再求值：
，其中：
四、解方程：（每小题6分，共12分）
（1）
（2）
五、（每小题8分，共16分）
1、关于x的一元二次方程mx2－(3m－1)x + 2m－1=0的根的判别式的值为1，求m的值及该方程的根。
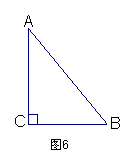
2、如图6是一个直角三角形材料，现要在上面截一个正方形。
要求：以C为一个顶点，其余三个顶点分别在BC、AB、AC边上，请你用尺规作图方法，画出所要求的正方形。（不写画法，保留作图痕迹）
 |
六、（每小题8分，共24分）
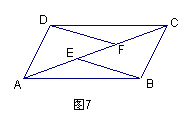1、如图7，已知E、F是
ABCD的对角线AC上两点，AE = CF。
求证：BE = DF
2、如图8，已知DC∥AB，且DC =AB，E为AB的中点。
（1）
求证：
。
（2）
观察图形，在不添加辅助线的情况下，除
外，还有与
的面积相等的三角形吗？若有请写写。
3、盒子里装三个红球，二个黄球和一个蓝球，它们除颜色外完全相同。
（1）从盒子里任意摸出一个球，出现哪种颜色的球的概率最大？为什么？
（2）从盒子里任意摸出两个球，可能会出现哪些结果？
七、（每小题10分，共20分）
1、如图9，在⊙O中，
，AB=3，AE·ED=5
（1）
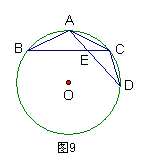求证：△AEC ∽ △ACD。
（2） 求EC的长。
2、如图10，用同样规格的黑白两色的正方形瓷砖铺设矩形地面，请观察图形并解答下列问题。
 |  |  | |||
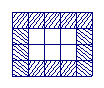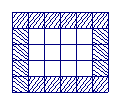n =1 n = 2
n = 3
(1) 在第n个图中，每一横行共有_____块瓷砖，每一竖列共有____块瓷砖。
(2) 按以上铺设方案，铺一块这样的矩形地面共用了506块瓷砖，求此时n的值。
(3) 若黑瓷砖每块4元，白瓷砖每块3元，在问题②中，共花多少钱购买瓷砖？
期末综合练习参考答案
一、1、A 2、D 3、B 4、A 5、C 6、A 7、D 8、C 9、B
10、C 11、C 12、D 13、B 14、D 15、B 16、D
二、1、4×10－5 2、－12xy 3、简单的随机抽样 4、8 5、
6、100cm2
三、1、5 2、
，当时，原式=
四、（1）
(2) 
五、1、由（3m－1）2－4m(2m－1) = 1，得m1=2, m2 =0(不合题意，应舍去)
故m =2。此时原方程的根为
2、提示：作CD平分∠ACB交AB于D，再作DE⊥AC于E，作DF⊥BC于F。CEDF就是所求作的正方形。
六、1、证：∵ ABCD是平行四边形
∴ AB
CD
∴ ∠DCF=∠CAB
又∵ AE = CF
∴ 
∴BE = DF
2、（1）∵ DC =AB，E为AB的中点
∴ AE = BE =DC
又∵ DC∥AB
∴ ∠AED = ∠B BEDC是平行四边形
∴ ED =BC
∴
（2）
3、（1）
出现红球的概率最，因为
（2） 一红一黄，一红一蓝，一黄一蓝，两个红球，两个黄球。
七、1、（1）∵ 
∴ ∠ACB = ∠ADC
又∵ ∠EAC = ∠CAD
∴ △AEC ∽ △ACD
（2）∵
∴ AC = AB = CD = 3 ∠ECA = ∠EAC
∴ AE = EC
∵ △AEC ∽ △ACD
∴ 
故 AC2 = AE·AD
AC2 = AE（AE + ED）
AC2 = AE2 + AE·ED
∵ AC = 3 AE·ED = 5
∴ AE2 = 4
故 AE = 2 = EC
2、（1）n + 3 , n + 2
（2）由题意，得（n +3）(n+2) = 506
解之,n1 =－25(舍去) n2 =20
（3）需白瓷砖：20×（20 +1）= 420（块）
故共需黑瓷砖：506－420 =86（块）
在问题（2）中，购买瓷砖共花费：420×3 + 86×4 = 1604（元）
答：共花1604元钱购买瓷砖。