第一学期初三数学期末考试
（总分：120分） 姓名： 成绩：
一、填空题：（每空3分，共30分）
1、（
）-2= 。
2、若分式
的值为0，则x=
。
3、当m= 时，方程
是一元二次方程。
4、如果方程3x2+x+a=0有实数根，则a的取值范是 。
5、关于
的一元二次方程
的一个根是0，则
的值为 。
6、抛物线
的顶点坐标为
。
7、正方形ABCD的边长是2cm,以直线AB为轴旋转一周，所得到的圆柱的侧面积
为 cm2.
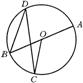
8、如图、AB是⊙O的直径，弦CD⊥AB,垂足为P，如AP∶PB=1∶4,CD=8,则AB= .
C
A P O B(8题)
(9)
D
9、如图，在⊙O中，AB是⊙O的直径，∠D＝40°，则∠AOC的度数为_____ _
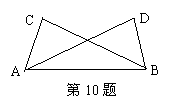
10、如图,已知AC=BD,则再添加条件 ,可证出△ABC≌△BAD.
二、选择题：（3×8=24分）
1、下列运算正确的是( )
A、 
B、 
C、 
D、 
2、计算
的结果是(
)
(A)
(B)
(C)
(D)
3、抛物线y=
的对称轴是（ ）
（A）x=-2 （B）x=2 （C）x=-4 （D）x=4
4、下列说法正确的是（ ）
（A）三点确定一个圆 （B）长度相等的弧是等弧
（C）一个圆只有一个内接三角形 （D）一个三角形只有一个外接圆
5、关于的方程
有两个不相等的实数根，则
的取值范围是（ ）
A．
B．
C．
D．
6、若圆锥的母线长为4cm，底面半径为3cm，则圆锥的侧面展开图的面积是（ ）
（A）
； （B）
； 
（C）
； （D）
；
7、一个直角三角形斜边长为
，内切圆半径为
，则这个三角形周长是（ ）
A、
B、
C、
D、
8、下列说法：（1）顶角和腰对应相等的两个等腰三角形全等 （2）顶角和底边对应相等的两个等腰三角形全等 （3）斜边对应相等的两个等腰直角三角形全等 （4）两个等边三角形全等 其中正确的说法共有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
三、解答题：（66分）
1、（4分）计算: 
2、（4分）解方程：x2+2x-3=0。
3、解方程：
（4分） 4、解方程
（4分）
5、化简：
（4分）
6、（6分）已知：关于x的方程x2-kx-2=o①、求证：方程有两个不相等的实数根。②、设方程的两个根为x1,x2如果2（x1+x2）>x1x2,求k的取值范围。
7、（6分）画图：（1）已知一等腰三角形的底边长和腰长，求作等腰三角形。
|
 | |||
 | |||
|
 |
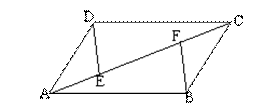8、（5分）如图，在平形四边形ABCD中，E、F是对角线AC上的两点，且AE=CF。
求证：DE=BF
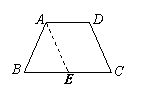
9、（6分）同一底上的两底角相等的梯形是等腰梯形吗？如果是，请给出证明（要求画出图形，写出已知、求证、证明）；如果不是，请给出反例（只需画图说明）.
10、（7分）如图，PA切⊙O于点A，PBC交⊙O于点B、C，若PB、PC的长是关于x的方程
的两根，且BC=4，求（1）m的值；（2）PA的长；
11、（8分）今年五月，某工程队（有甲、乙两组）承包人民路中段的路基改造工程，规定若干天内完成．（1）已知甲组单独完成这项工程所需时间比规定时间的2倍多4天，乙组单独完成这项工程所需时间比规定时间的2倍少16天．如果甲、乙两组合做24天完成，那么甲、乙两组合做能否在规定时间内完成？（2）在实际工作中，甲、乙两组合做完成这项工程的
后，工程队又承包了东段的改造工程，需抽调一组过去，从按时完成中段任务考虑，你认为抽调哪一组最好？请说明理由．
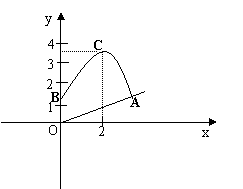
12、（8分）某农场为防风治沙，在一山坡上种植一片树苗，并安装了自动喷灌设备。已知喷水头喷出的水流成抛物线形，如图所示建立直角坐标系。已知喷水头B高出地面1.5米，水流最高点C的坐标为（2，3.5），喷水管与山坡的夹角∠BOA约为63°，计算水喷出后落在山坡上的最远距离。
 |
参考答案：
一、填空题：
1、9； 2、x=1; 3、3; 4、a≤
; 5、-1；6、（-2，5）7、8
8、10； 9、100° 10、∠CAB=∠DBA或BC=AD
二、选择题：BDBDABBC
三、解答题：
1、4-8×0.125+1+1=5 2、（x-1）(x+3)=0 x1=1,x2= -3 3、3x2+x-2=0 x1=
-1,x2=
4,3(x-1)-(x+3)=0 2x-6=0 x=3,经检验是原方程的解。
5、
6、①、Δ=k2+8 ∵k2≥0 ∴k2+8>0.∴方程有两个不相等的实数根。…………（3分）
②、∵x1+x2=k,x1x2= -2 ∴2k>-2 ∴k>-1……………………（3分）
7、略 8、∵平行四边形ABCD∴AD=BC,DC∥AB,…………（2分）
∴∠DAE=∠BCF,AE=CF.∴ΔDAE≌ΔDAF……（2分）,∴DE=CF.…………（1分）
9、是等腰梯形……………………………………………………………………………………（1分）
已知：梯形ABCD，AD∥BC且∠B=∠C（或∠A=∠D）………………………………（2分）
求证：梯形ABCD是等腰梯形……………………………………………………………（3分）
证明一：过点A作AE∥DC，交BC于E…………………………（4分）
∵AD∥BC AE∥DC
∴四边形AECD是平行四边形，∴∠AEB=∠C，
AE=DC…………………………………………………（5分）
∵∠B=∠C
∴∠AEB=∠B………………………………………………………………………（6分）
∴AB=AE……………………………………………………………………………（7分）
∴AB=DC
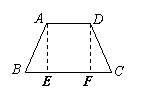∴梯形ABCD是等腰梯形………………………………………………………（8分）
证明二：过A、D两点分别作AE⊥BC，DF⊥BC垂足为E、F
∵AE⊥BC、DF⊥BC
∴AE∥DF且∠AEB=∠DFC
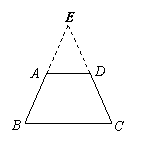∵AD∥BC
∴四边形AEFD是平行四边形 ∴AE=DF
∵∠AEB=∠DFC ∠B=∠C
∴△AEB≌△DFC ∴AB=DC
∴梯形ABCD是等腰梯形
证明三：延长BA、CD交于E点
∵∠B=∠C ∴BE=CE
∴AD∥BC ∴∠EAD=∠B，∠EDA=∠C ∴∠EAD=∠EDA
∴AE=DE ∴AB=DC
∴梯形ABCD是等腰梯形
10、 解：由题意知：（1）PB+PC=8，BC=PC－PB=2 ………………（1分）
∴PB=2，PC=6……………………（2分）
∴PB·PC=(m+2)=12
∴m=10 ………………（2分）
（2）∴PA2=PB·PC=12
∴PA=
…………（2分）
11.解：（1）设规定时间为x天，则
解之，得x
=28，x
=2………………（2+1+1分）
经检验可知x=28，x=2都是所列方程的根，但x=2不合题意，舍去，只取x=28
由24＜28知，甲、乙两组合做可在规定时间内完成．
（2）设甲、乙两组合做完成这项工程的
用去了y天，则
解之，得y=20（天）………………（2分）
甲独做剩下工程所需的时间：
（天）
∵20+10=30＞28，∴甲独做剩下的工程不能在规定时间内完成；…………（1分）
乙独做剩下工程所需的时间：
（天）
∵20+6
=26＜28，∴乙独做剩下的工程能在规定时间内完成．
∴我认为抽甲组最好．………………（1分）
12、设
显然B（0，1.5）……………………（2分）
将点B坐标代入，解得
………………………………………（1分）
……（2分）
由
和
联立方程组，解得
……（1分）
米……………………（2分）