九年级第一学期期末试卷
一、选择题:(本题共12分,每小题3分)
在每题的四个备选答案中只有一个是正确的,请将正确答案前的字母填在括号中。
1. 已知两圆的半径分别为3和5,且它们的圆心距为8,则这两个圆的位置关系为( )
A. 外离 B. 外切
C. 相交 D. 内含
2. 已知数据3,5,x,10的平均数是6,则x的值为( )
A. 4 B. 5 C. 6 D. 7
3. 在图形“圆,平行四边形,矩形,正方形”中,既是轴对称图形又是中心对称图形的有( )
A. 一个 B. 两个
C. 三个 D. 四个
4. 如图1,已知⊙O中,半径OC垂直于弦AB,垂足为D,若OD=3,OA=5,则AB的长为( )
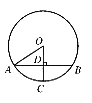
图1
A. 2 B. 4 C. 6 D. 8
二、填空题:(本题共24分,每空4分)
5. 已知一个圆形细菌的直径长约为0.000015米,那么这个细菌的直径长用科学记数法表示为______________米。
6. 已知分式![]() 的值为零,那么x的值为______________。
的值为零,那么x的值为______________。
7. 若方程![]() 是关于x的一元二次方程,则m的取值范围是______________。
是关于x的一元二次方程,则m的取值范围是______________。
8. 投掷一枚质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体的玩具),掷一次得到点数为“4”的概率为______________。
9. 有一张圆形的纸片,如果不借助作图工具找它的圆心,你的方法是______________
________________________________________________________。
10. 如图2,这是一个滚珠轴承的示意图,其中内、外圆的半径分别为2和6,如果在内、外圆之间放半径为2的滚珠(有阴影的圆表示滚珠),请你猜想在内、外圆之间最多可以放______________个滚珠。
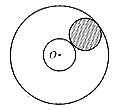
图2
三、解答题:(本题共36分,每小题6分)
11. 解方程![]()
12. 计算:![]()
13. 计算:![]()
14. 已知:如图3,AB∥CD,AE=DF,AB=CD。
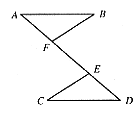
图3
求证:△ABF≌△DCE
15. 已知:如图4,点C是∠APB平分线PD上一点,PA=PB。
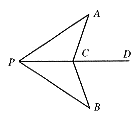
图4
求证:∠ACD=∠BCD
16. 已知:如图5,在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE,若CD与BE交于P点。
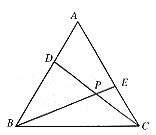
图5
求证:∠DPB=60°。
四、作图与解答题:(本题8分)
17. 已知:如图6,∠α。(作图要求保留作图痕迹)
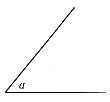
图6
(1)求作:∠ABC,使∠ABC=∠![]() ;(2分)
;(2分)
(2)如图7,求作:∠ABC的平分线BD;(2分)
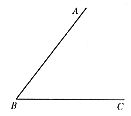
图7
(3)如图8,O是∠ABC的平分线BD上任意一点,以O为圆心的⊙O与BC相切于E点。
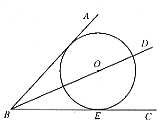
图8
说明⊙O与AB相切。(4分)
五、解答题:(本题10分,每小题5分)
18. 已知关于x的方程![]() 的一个根为2,且
的一个根为2,且![]() ,求
,求![]() 的值。
的值。
19. 已知:如图9,为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及![]() 的弧长。
的弧长。
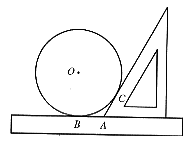
图9
六、(本题20分,每小题5分)
20. 已知在关于x的一元二次方程![]() 中,如果系数b与c在2、3、4中取值(同一方程中的两个系数取不同的数值),写出取值后所有相应的方程,并确定所得的方程中有实数根的方程,再说明你的理由。
中,如果系数b与c在2、3、4中取值(同一方程中的两个系数取不同的数值),写出取值后所有相应的方程,并确定所得的方程中有实数根的方程,再说明你的理由。
21. 已知:如图10,扇形OAB与扇形OCD有一部分叠放在一起,且它们的圆心角都是90°,连结AC、BD,若OA=3,OC=1,求阴影部分的面积。
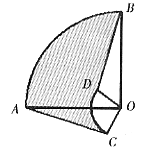
图10
22. 如图11,这是圆桌正上方的灯泡O(把灯泡看作一个点),发出的光线照射在桌面后在地面上形成阴影的示意图,已知桌面直径为1.2米,桌面距地面1米,若灯泡离地面2.5米,求地面上阴影部分的面积。
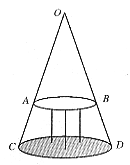
图11
23. 参加同一射击项目的两位运动员张明、王成在一次打靶中的成绩,如图12(1)(张明)、图12(2)(王成)所示(图中的各点分别表示每一次打靶的环数):
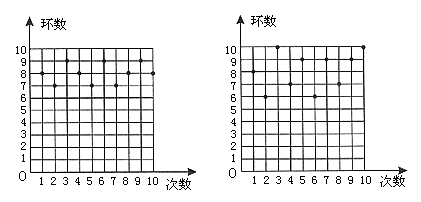
(1) (2)
图12
利用图中提供的信息,解答下列问题:
(1)完成表格的填写;
(2)如果将9环以上(含9环)视为优秀,则优秀率高的运动员是_____________;
(3)根据所学的统计知识,利用图与表中的数据评价这两位运动员此次打靶的发挥情况。
| 姓名 | 平均成绩 | 中位数 | 众数 | 方差 |
|
|
|
|
|
|
|
|
|
|
|
|
七、解答题:(本题10分,第24题4分,第25题6分)
24. 已知AB是半圆的直径,CD∥AB,AB=4,求:(1)如图13(1),若C、D是半圆上的三分之一点,求阴影部分的面积;(2)如图13(2),若点P是BA延长线上的点,PC是切线,当其他条件不变时,说明此图中的阴影部分的面积与图1中阴影部分面积之间的关系。
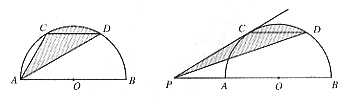
(1) (2)
图13
25. 已知一块直径为2米的半圆形铁皮,现要在充分利用这块铁皮的前提下,加工出一个圆锥的底面与一个圆柱的两个底面,请你选择下列其中一种加工方案,并求出此方案中各底面的半径长,再判断四个圆心构成的四边形是什么四边形。
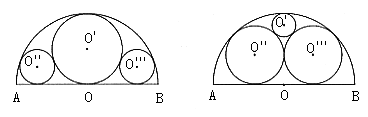
(1) (2)
图14
(1)方案一:如图14(1),当圆锥的底面最大时;
(2)方案二:如图14(2),当圆柱的底面最大时。
【试题答案】
一、选择题:
1. B 2. C 3. C 4. D
二、填空题:
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. 用两次不同的对折重合的方法,折痕的交点是圆心
10. 6
三、解答题:
11. 解:原方程化为![]() 2分
2分
所以 ![]() 6分
6分
12. 解:![]()
![]() 2分
2分
![]() 6分
6分
13. 解:原式![]() 3分
3分
![]() 6分
6分
14. 证明:因为AB∥CD,
所以 ∠A=∠D 1分
因为 AE=DF,
所以 AF=DE 2分
在△ABF与△DCE中,
AB=CD,∠A=∠D,AF=DE,
所以△ABF≌△DCE 6分
15. 证明:因为PD是∠APB的平分线,
所以 ∠ACP=∠BCP 1分
在△ACP与△BCP中,
PC=PC,∠ACP=∠BCP,PA=PB,
所以 △ACP≌△BCP 3分
所以∠ACP=∠BCP 5分
因为∠ACP+∠ACD=180°,∠PCB+∠BCD=180°,
所以∠ACD=∠BCD 6分
16. 证明:在等边三角形ABC中,
AC=BC,∠A=∠ACB=60° 1分
在△DAC与△ECB中,
AD=EC,∠A=∠ACB,AC=BC
所以 △DAC≌△ECB 4分
所以 ∠ACD=∠EBC 5分
故 ∠DPB=60° 6分
17. 解:(1)保留了作图痕迹,作图正确的不扣分;
(2)保留了作图痕迹,作图正确的不扣分;
(3)“过点O作AB的垂线交AB于点F”,给1分,证明正确的给满分。
18. 解:根据条件,方程的一个根为![]() ,
,
可得 ![]() 1分
1分
又![]() ,即
,即![]()
由非负数的性质可知(a,b的值可分别给分),
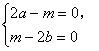 2分
2分
则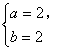 4分
4分
所以 ![]() 5分
5分
19. 解:连结OB、OC、OA
因为AB、AC是切线,与圆相邻的三角板的内角为60度,
所以AB=AC,∠BAO=∠CAO=60° 2分
由AB=5cm
可得 ![]() cm及
cm及![]() 的弧长为
的弧长为![]() 5分
5分
20. 解:由条件有(下列方程书写不全的扣1分)
![]() ,
,
![]() 2分
2分
![]()
其中有实数根的方程,有(没有写全的扣1分)
![]() 4分
4分
理由:它们的根的判别式都大于零。 5分
21. 解:由题意与图形条件,有
在△AOC与△BOD中
OC=OD,∠AOC=∠BOD(可证),AO=BO,1分
所以△AOC≌△BOD 3分
因此,阴影部分的面积等于两个圆心角为90°的扇形OAB与扇形OCD的面积之差。
所以 阴影部分的面积等于![]() 5分
5分
22. 解:连结AB、CD,过点O作OE⊥CD于E,交AB于F。 1分
由题意,有AB∥CD,OC=OD以及点E、F分别是桌面与地面阴影的圆心
可证 △OFB∽△OED 2分
所以 ![]() 3分
3分
可求得ED的长为1米 4分
即可求得 阴影部分的面积为![]() 平方米 5分
平方米 5分
23. 解:(1)填表全对的满分,错两个扣1分; 3分
(2)依题意答对的不扣分; 4分
(3)根据题中给出的数据,评价正确的满分。 5分
24. 解:(1)连结OC、OD
根据题中的条件,CD∥AB,可得
![]() 2分
2分
所以 阴影部分 ![]() 3分
3分
(2)由于点P在平行线上,
所以 图2中的阴影部分的面积等于图1中的阴影部分的面积。 4分
25. 解:方案一:
由于圆锥底面的圆最大(即此圆与半圆及直径相切),圆柱底面的圆较小(两个等圆分别与⊙O'及半圆、AB相切),如图,
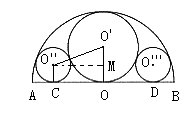
连结OO'、O'O''、O''C,过点O''作O''M⊥O'O于点M。 2分
则有圆锥的底面直径为1,设圆柱的底面半径为x
则有 ![]()
解得 ![]() 4分
4分
可证明由四个圆心构成的四边形是菱形 6分
方案二:由于圆柱底面的圆最大,圆锥底面的圆较小,如图,
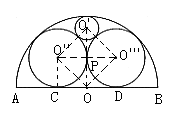
连结![]()
设圆柱底面的半径为x
则根据题意,有![]() ,而
,而![]()
由勾股定理,有![]()
则![]() 2分
2分
设圆锥底面的半径为y
进而,有 ![]()
![]()
解得 ![]() 4分
4分
可证由四个圆心构成的四边形是正方形。 6分