初三数学第一学期期末质量检查
学校： 班级： 姓名： 座号：
| 题 号 | 一 | 二 | 三 | 四 | 五 | 合 计 |
| 得 分 |
［说明］本卷满分120分，考试时间100分钟。
一、 填空题（每小题3分，共24分）
1、计算：
=
2、当x
时，分式
有意义。
3、一元二次方程
的根为
。
4、若关于x的一元二次方程
的一个根为1，则m的值为
。
5、国家质检总局出台了国内销售纤维制品的甲醛含量标准，从2003年1月1日起正式实施。该标准规定针织内衣，被套、床上用品等直接接触皮肤的制品甲醛含量应在百万分之七十五以下，百万分之七十五用科学记数法表示应写成
。
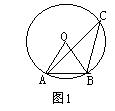
6、如图1：AB是⊙O的弦，
AOB是等边三角形，C是⊙O上
一点，则∠C= 度
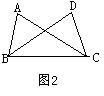
7、如图2：已知AB=DC，要使得ABC≌DCB，只需
添加的一个条件为 （写一个即可）
8、为增强同学们的环保意识，某校家住南小区的50名初三学生调查某
一天各自家庭丢弃塑料袋的情况，统计结果如下：
| 丢弃塑料袋（个） | １ | ２ | ３ | ４ | ５ |
| 户 数 | ３ | ６ | ２０ | １５ | ６ |
若该小区约有１．５万户居民，则该小区所有家庭每天丢弃塑料袋总数为 万个．
二、选择题（每小题４分，共２４分）
９、一元二次方程
的根的情况为（ ）
Ａ、有两个不相等的实数根 Ｂ、有两个相等的实数根
Ｃ、没有实数根 Ｄ、无法确定
10、下列计算正确的是（ ）（ａ
０）
Ａ、
Ｂ、
Ｃ、
Ｄ、
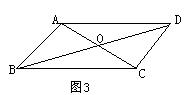11、如图３：Ｏ是平行四边形对角线的交点，则图中全等的三角形为（ ）
Ａ、２对 B、３对 C、４对 D、５对
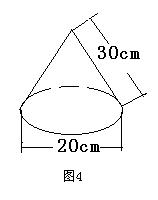12、如图４：是小明制作的一个圆锥型纸帽的示意图，则围成这个
纸帽所用的纸的面积为（ ）ｃｍ２（不计粘贴部分）
Ａ、１５０л Ｂ、３００л Ｃ、４００л Ｄ、６００л
13、已知两圆的圆心距为４，半径分别为Ｒ和ｒ，且Ｒ和ｒ是方程
的两个根，则这两个圆的位置关系为（ ）
Ａ、相交 Ｂ、外离 Ｃ、内切 Ｄ、外切
14、某牧羊区为了估计该区黄羊的只数，先捕促２０只黄羊给它们分别做上标记，然后放还，待有标记的黄羊完全混合在羊群后第二次捕捉４０只黄羊，发现其中２只有标记，从而可估计该牧羊区有黄羊（ ）
Ａ、４００只 B、３００只 C、２００只 D、１００只
三、解答下列各题（每小题６分，共３０分）
１５、计算：
１６、先化简，再求值：
。
１７、解分式方程： 
１８、若ｘ１，、ｘ２是方程
的两个实数根，不解方程，求下列各式的值。
（１） （ｘ１＋ｘ２）－ｘ１ｘ２： （２）
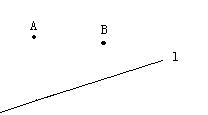
１９、作图题：已知Ａ、Ｂ两点和直线ｌ，求作⊙Ｏ，使⊙Ｏ经过Ａ、Ｂ两点，且圆心在直线Ｌ上
（保留作图痕迹，不要求写作法与证明）。
四、解答下列各题：（每小题８分，共２４分）
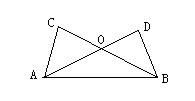
２０、如图：ＡＤ⊥ＢＤ于Ｄ，ＢＣ⊥ＡＣ于Ｃ，，ＡＣ＝ＢＤ，ＡＤ与ＢＣ相交于点Ｏ，
求证：ＯＡ＝ＯＢ
２１、用２０ｃｍ长的铁丝能否折成面积为３０ｃｍ２矩形，若能够，求出它的长和宽；若不能，请说明理由。
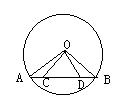
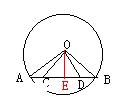
２２、如图：已知，在⊙Ｏ中，ＡＢ是弦，Ｃ、Ｄ两点在ＡＢ上，且ＡＣ＝ＢＤ
求证：ＣＯＤ是等腰三角形（请用两种方法证明，每种证法得４分）
五、解答下列各题（每小题９分，共１８分）
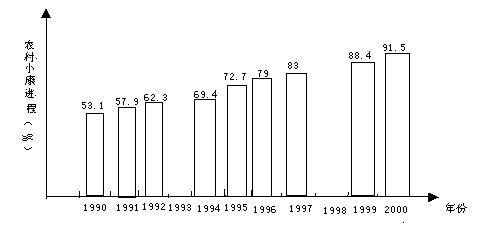
２３、阅读下列材料，下图表示我国农村居民小康生活水平的实现程度。
地处西部的某贫困县，农村人口约５０为万，２００２年农村小康生活的综合实现程度仅达到
６８％，即没有达到小康程度的人口为（１－６８％）×５０＝１６万。
解答下列问题：
（１） 假设该县计划在２００２年的基础上，到２００４年底，使没有达到小康程度的１６万农村人口降至１０.２４万，那么平均每年降低的百分率是多少？
（２） 如果该计划实现，２００４年底该县农村小康进程接近上图中哪一年的水平（假设该县人口２年内不变）？
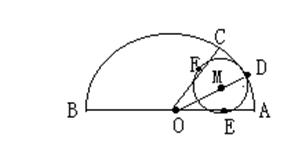
２４、如图：有一个半径为R的半圆，要用这个半圆做一个圆锥的侧面和底面，小芳想这样做：在圆弧上取点C，使∠AOC=600，用扇形OBC作圆锥的侧面，在扇形OAC内剪一个最大的⊙M作圆锥的底面，你认为小芳这样做办得到吗？请你通过计算说明理由。
参考答案
一、填空题
1、
x： 2、x≠1； 3、
；4、m=2； 5、7.5×10-5；6 、30；
7、AC=DB（或∠ABC=∠DCB）；8、4.95；
二、选择题；
9、A； 10、B； 11、C； 12、B； 13、D； 14、A；
三、解答下列各题
15、解：原式=1+4+1+4=10
16、解：原式=
=
=
；当
时，原式==
17、解：方程两边同时乘以x（x+3）得
解得，x=6
经检验：x=6是原方程的解，所以原方程的解为x=6；
18、解：依题意得，（ｘ１＋ｘ２）=5，ｘ１ｘ２=-8，（1）（ｘ１＋ｘ２）－ｘ１ｘ２=13
（2）=
=
19、作AB的垂直平分线得3分，作⊙O得2分，结论得1分
四、解答下列各题
20、证明：∵AC=BD，AB=BA，∴RtACB≌RtBDA
∴∠ABC=∠BAD，∴ＯＡ＝ＯＢ
21、解：不能
设一边长为x，则另一边为10-x，依题意得
x（10-x）=30，整理得：x2-10x+30=0
∵=100-120=-20＜0∴方程x2-10x+30=0无实数根，∴不能折成满足条件的矩形；
22、证明一：∵OA=OB，∴∠A=∠B，又∵AC=BD，∴AOC≌BOD
∴ OC=OD，∴COD是等腰三角形分
证明二：作OE⊥AB于E，则AE=BE，∵AC=BD ∴CE=DE
∵OE=OE ， ∠OEC=∠OED=900
∴COE≌DOE
∴OC=OD ∴COD是等腰三角形分
五、解答下列各题
23、（1）解：设平均每年降低的百分率为x，依题意得，
所以， 
解得，x1 =0.2 x2=1.8（不合题意，舍去）
答：平均每年降低的百分率为20%。
（２）
：因为 
，所以2004年该县农村小康进程接近1996年的水平。
24、解：连结OE，∵⊙M与OA相切于E,∴ME⊥OA
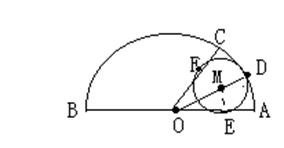设 ⊙M 的半径为r，∵∠MOE=
∠AOC=300
∴OM=2r
∵2r+r=R ∴r=
R, ∴⊙M的周长
而弧BC=
，∴小芳这样办得到。