九年级(上)数学阶段测试（月考）（附答案）

　　九年级数学阶段测试（月考）（附答案）　　2006.10

（满分150分；完卷时间120分钟）

班级　　　　  姓名　　　　　　　 　　　　成绩　　　　　　 

一．选择题（每题4分，共48分）

1、下列各式中，y是的二次函数的是( 　　)

A． 　 B．　　C．  　　D．

2、反比例函数的图象在　(　　　)

(A)第一、三象限　(B)第二、四象限　　(C)第一、二象限　　(D)第三、四象限

3、已知抛物线的解析式为y＝(x－2)²＋1，则抛物线的顶点坐标是( 　　)

A、(－2，1)　　 B、(2，1)　　　 C、(2，－1)　　　　 D、(1，2)

4、抛物线向右平移1个单位，再向上平移2个单位，得到新的图象的二次函数表达式是(　　)　　　　　 

 A 　　　B 　

C　　　 

D　

5、抛物线则图象与轴交点为（　　 ）

A． 二个交点　　　 B．　一个交点　 　 C． 　 无交点　 D．　不能确定

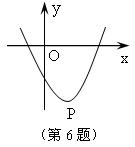
6、如图，抛物线的顶点P的坐标是(1，－3)，则此抛物线对应的二次函数有（　　　）

(A)最大值1　　　　　 (B)最小值－3

(C)最大值－3　　　　  (D)最小值1

7、根据下列表格的对应值：

x	3.23	3.24	3.25	3.26
y=ax2+bx+c	-0.06	-0.02	0.03	0.09

判断方程ax²+bx+c=0（a≠0,a、b、c为常数）一个解的范围是　（　　　　）

Ａ、3＜x＜3.23　　Ｂ、3.23＜x＜3.24　 Ｃ、3.24＜x＜3.25　　 Ｄ、3.25＜x＜3.26

8、已知是反比例函数的图象上三点，且，则的大小关系是（　　）

A、　　　　　　　　  B、　

C、　　　　　　　　  D、

9、二次函数的图象如图所示，则下列结论正确的是（　　　 ）

A、a>0　 b<0　 c>0　　 B、a<0　 b<0　 c>0

C、a<0　 b>0　 c>0　　 D、a<0　 b>0　 c<0

10、已知电压为220伏保持不变 ，则电流 y 与电阻 x 之间的关系用图象大致可表示为

　　　　 

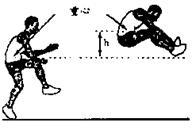11、小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数(t的单位：s，h的单位：m)可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是(　　　)

(A)0.71s　 (B)0.70s　 (C)0.63s　　(D)0.36s

12、如图所示，　，则反比例函数的解析式是（　　　　）

y

A

A、　　  B、　　　　　　 

o

x

B

C、　　　 D、

二．填空题：（每题5分，共30分）

13、已知反比例函数y＝的图象经过点(1，2)，则k的值是_________。

14、 请写出一个开口向上，且对称轴为直线的二次函数解析式 　　　　　　　　。

15、对于函数，当时，y的取值范围是____________；

16、已知抛物线的顶点在轴上，则的值是　　　　  。

17、经市场调查，某种商品的进价为每件6元，专卖商店的每日固定成本为150元。当销售价为每件10元时，日均销售量为100件，单价每降低1元，日均销售量增加40个。设单价为x元时的日均毛利润为y元，则y关于x的函数解析式为_____________________。（只需列式）

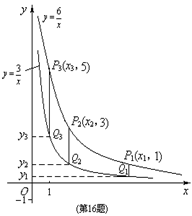18、　两个反比例函数，在第一象限内的图象如图所示, 点P₁，P₂，P₃，…，P_{2 005}在反比例函数图象上，它们的横坐标分别是x₁，x₂，x₃，…，x_{2 005}，纵坐标分别是1，3，5，…，共2 005个连续奇数，过点P₁， P₂，P₃，…，P_{2 005}分别作y轴的平行线，与的图象交点依次是Q₁（x₁，y₁），Q₂（x₂，y₂），Q₃（x₃，y₃），…，Q_{2 005}（x_{2 005}，y_{2 005}），

则y_{2 005}=　　　　　 ．

三．解答题(共72分)

19、（8分）若一个面积为20cm²的矩形的宽y（cm），长x（cm）。

（1）直接写出y与x的函数关系式，以及自变量x的取值范围。

（2）在右方格中用描点法画出所求函数的图象。

（2）当长满足5≤x≤10时，求宽y的取值范围。

　　　　　 

20、（6分）求二次函数y=x²+2x-4图象的开口方向、对称轴、顶点坐标。

21、（6分）已知是的反比例函数，当=3时，=4，则当=2时求函数的值。

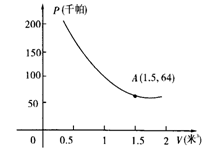22、（8分）某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米²)的反比例函数,其图象如图所示(千帕是一种压强单位)

（1）写出这个函数的解析式；

（2）当气球的体积为0.8立方米时,气球内的气压是多少千帕？

（3）当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米？

23、（8分）已知正比例函数与反比例函数的图象都过A（ｍ，1）点。

（1）求m的值，并求反比例函数的解析式。（6分）

（2）求正比例函数与反比例函数的另一个交点B的坐标。（2分）

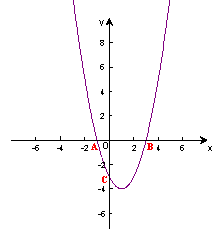24、（12分）在直角坐标平面中，O为坐标原点，二次函数的图象与x轴的负半轴相交于点C（如图5），点C的坐标为（0，－3），且BO＝CO

（1）　　　 求出B点坐标和这个二次函数的解析式；

（2）　　　 求△ABC的面积。

（3）　　　 设这个二次函数的图象的顶点为M，求AM的长.

25、（12分）农民张大伯为了致富奔小康，大力发展家庭养殖业，他准备用40米长的木栏围一个矩形的养圈，为了节约材料，同时要使矩形面积最大，他利用了自己家房屋一面长25米的墙，设计了入图一个矩形的养圈。

（1）请你求出张大伯设计的矩形羊圈的面积。

（2）请你判断他的设计方案是否使矩形羊圈的面积最大？如果不是最大，应怎样设计？请说明理由。　　　　　　　　　　　　　　　　　　　　　　

26、（12分）右图是泰州某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．若把拱桥的截面图放在平面直角坐标系中(如下图)．

(1)求抛物线的解析式.(7分)

(2)求两盏景观灯之间的水平距离.(5分)

答案：

一、CABAB　BCDCB　BA

二、13、2　 14、略 15、0，1 16、2 17

18、2004.5

三、19、 (1)xy=20()

　　　　　　　 (2)略

　　　　　　  （3）

20、开口向上,对称轴：直线x=-1,顶点坐标(-1,-5)

21、6

22、

（1）

（2）120

（3）

23、（1）m=3,

（2）(-3,-1)

24、(1)B(3,0),

(2)6

(3)

25、（1）187.5

（2）宽为10米时，面积最大为200平米

26、(1)

(2)5