九年级(上)数学单元测试卷
第一章 证明(二)
班级 姓名 成绩
一、选择题(每小题3分，共30分)
1、已知△ABC的三边长分别是3cm、4cm、5cm，则△ABC的面积是（ ）
A.6cm2 B.7.5cm2 C.10cm2 D.12cm2
2、下列判断正确的是（ ）
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等，且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
3、具有下列条件的两个等腰三角形，不能判断它们全等的是（ ）
A.顶角、一腰对应相等 B.底边、一腰对应相等
C.两腰对应相等 D.一底角、底边对应相等
4、在平面直角坐标系xoy中，已知A（2，–2），在y轴上确定点P，使△AOP为等到腰三角形，则符合条件的点P共有（ ）
A.2个 B.3个 C. 4个 D.5个
5、到△ABC的三个顶点距离相等的点是△ABC的（ ）
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边中垂线的交点
6、角平分线的尺规作图，其根据是构造两个全等三角形，由作图可知：判断所构造的两个三角形全等的依据是（ ）
A.SSS B.ASA C.SAS D.AAS
7、一架长2.5m的梯子，斜立在一竖直的墙上，这时梯子底端距墙底端0.7m，如果梯子的顶端沿墙下滑0.4m，那么梯子底端将滑动（ ）
A.0.9m B.1.5m C.0.5m D.0.8m
8、△ABC中，∠A∶∠B∶∠C=1∶2∶3，CD⊥AB于点D若BC=a，则AD等于（ ）
A.
a B.
a C.
a D.
a
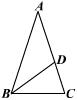
9、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）
A.30° B.36° C.45° D.70°
 | |||||||
 | |||||||
 | |||||||
 | |||||||
(第9题图) (第10题图) (第11题图) (第12题图)
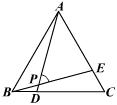
10、如图，等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（ ）
A.45° B.55° C.60° D.75°
二、填空题(每小题3分，共30分)
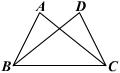
11、如图，已知AC=DB，要使△ABC≌△DCB，只需增加的一个条件是 或 .
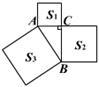
12、如图，△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S1、S2、S3分别表示着三个正方形的面积，S1=81，S3=225，则S2= .
13、等腰直角三角形的腰长为2cm，面积等于1cm2，则它的顶角的度数为 .
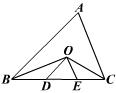
14、已知，如图，O是△ABC的∠ABC、∠ACB的角平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若BC = 10 cm，则△ODE的周长 .
15、如图，在Rt△ABC中，∠B=90°，∠A=40°，AC的垂直平分线MN与AB相交于D点，则∠BCD的度数是 .
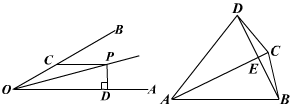
16、如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD的长为 .
17、等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a，则其底边上的高是 .
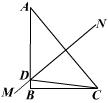
18、如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分DAB，且AB=AC，AC=AD，有如下四个结论：①AC⊥BD；②BC=DE；③∠DBC=∠DAB
；④△ABC是正三角形。请写出正确结论的序号
（把你认为正确结论的序号都填上）。
 |  | ||||
 | |||||
(第14题图) (第15题图) (第16题图) (第18题图)
三、(每小题6分，共12分)
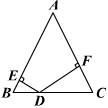
19、已知：如图，D是等腰ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF。当D点在什么位置时，DE=DF？并加以证明.
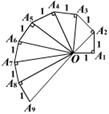20、如图是第七届国际数学教育大会的会徽。它的主题图案是由一连串如图所示的直角三角形演化而成的。设其中的第一个直角三角形OA1A2是等腰三角形，且OA1=A1A2=A2A3=A3A4=……=A8A9=1，请你先把图中其它8条线段的长计算出来，填在下面的表格中，然后再计算这8条线段的长的乘积。
| OA1 | OA2 | OA3 | OA4 | OA5 | OA6 | OA7 | OA8 |
四、(每小题8分，共18分)
21、如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：
(1) AD=CB；(2)AE=CF；(3)∠B=∠D；(4)AD∥BC。请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.
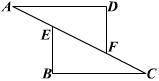
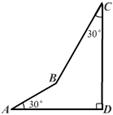
22、如图，AD⊥CD，AB=10，BC=20，∠A=∠C=30°，求AD、CD的长.
 |
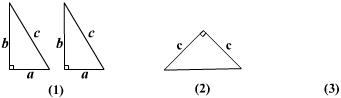
23、如图(1)是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c。图(2)是以c为直角边的等腰直角三角形。请你开动脑筋，将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图，指出它是什么图形.
(2)用这个图形证明勾股定理.
(3)假设图(1)中的直角三角形有若干个，你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗？请图(3)中画出拼后的示意图(无需证明).
 |
五、(本题10分)
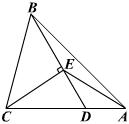24、如图，△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD，E为垂足，连结AE.
(1)写出图中所有相等的线段，并加以证明；
(2)图中有无相似三角形？若有，请写出一对；若没有，请说明理由；
(3)求△BEC与△BEA的面积之比.