专题一：规律探究
1.请看下列的一系列算式：
第一个：1＋3＝4＝22
第二个：1＋3＋5＝9＝32
第三个：1＋3＋5＋７＝16＝42
第四个：1＋3＋5＋７＋9＝25＝52……
根据上面各式的规律，请你写出第n个算式的表达式，并计算第20个式子的值．
2. 自然数中有许多奇妙而有趣的现象，很多秘密等待着我们去探索！比如：对任意一个自然数，先将其各位数字求和，再将其和乘以 3后加上1，多次重复这种操作运算，运算结果最终会得到一个固定不变的数R，它会掉入一个数字“陷井”，永远也别想逃出来，没有一个自然数能逃出它的“魔掌”.那么最终掉入“陷井”的这个固定不变的数R= .
3、将正奇数按一定的规律排列成5列， 第1列 第2列 第3列 第4列 第5列
根据已有的规律继续排下去，则数 第1行 1 3 5 7
2005在第 行，第 列。 第2行 15 13 11 9
第3行 17 19 21 23
第4行 31 29 27 25
|
33
4、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为
5. 有一列数：1，2，3，4，5，6，……，当按顺序从第2个数数到第6个数时，共数了_______个数；当按顺序从第m个数数到第n个数（
）时，共数了_______个数。
6. 观察下列各式：
；……请你将猜想到的规律用自然数
表示出来：____________________________。
7. 1～54这54个自然数排列如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| …… | |||||
| 49 | 50 | 51 | 52 | 53 | 54 |
在这张数表中任意圈出一个竖列上相邻的3个数，和不可能是（ ）
A. 66 B. 39 C. 40 D. 57
8. 观察下列两组算式：
（1）
，
（2）
，……
根据你发现的规律写出
的末位数字是（ ）
A. 2 B. 4 C. 8 D. 6
9、已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成下列形式：
第1行 1
第2行 －2 3
第3行 －4 5 －6
第4行 7 －8 9 －10
第5行 11 －12 13 －14 15
… …
按照上述规律排下去，那么第10行从左边数第5个数等于 ．
10、观察分析下列数据，按规律填空：
，2，
，2，
，…， 
(第n个数)。
11、观察下面的点阵图和相应的等式，探究其中的规律：
（1）在④和⑤后面的横线上分别写出相应的等式；
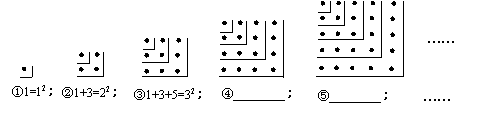
（2）通过猜想写出与第n个点阵相对应的等式.
12、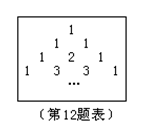
我国宋朝数学家杨辉在他的著作《祥解九章算法》中提出右表，此 表揭示了
（n为非负数）展开式的各项系数的规律。例如：
，它只有一项，系数为1；
，它有两项，系数分别为1，1；
，它有三项，系数分别为1，2，1；
，它有四项，系数分别为1，3，3，1；
……
根据以上规律，
展开式共有五项，系数分别为
。
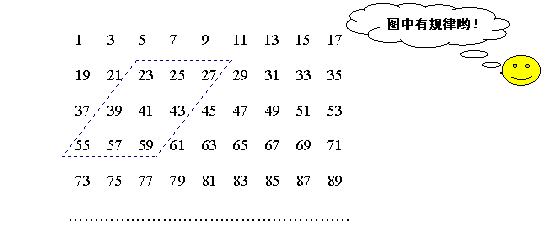
13、下图的数阵是由全体奇数排成
（1）图中平行四边形框内的九个数之和与中间的数有什么关系？
（2）在数阵图中任意作一类似（1）中的平行四边形框，这九个数之和还有这种规律吗？请说出理由；
（3）这九个数之和能等于1998吗？2005，1017呢？若能，请写出这九个数中最小的一个，若不能，请说出理由。
 |