第一学期期末考试九年级数学试卷华师大版

2005---2006学年第一学期期末考试试卷

九年级数学

学校 　　　　　　班级　　　　   姓名　　　　   得分　　　

一、真空题（每空2分，共10小题，满分28分）

1、　　　　。

2、若分式的值为零，则x的值为　　　　  。

3、一种细菌的直径是0.00004m，用科学记数法把它来表示为　　　　　  m。

4、若关于x的方程的两个根是-3和-1，则p=　　 ，q=　　　。

5、用换元法解方程时，如果设，那么原方程可转化为　　　　　　　　　　　 。

6、有一间长20米，宽15米的会议室，在它中间铺一块地毯，地毯的面积是会议室面积的一半，四周没铺地毯的留空宽度相同，则留空的宽度是　　　米。

7、如图1，MN所在的直线垂直平分线段AB，利用这样的工具，最少使用　 次，就可以找到圆形工件的圆心。

 

 

 

 

 

 

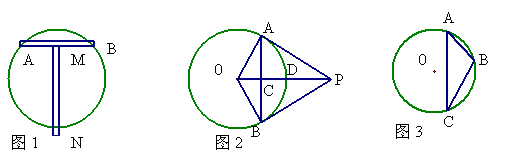
8、如图2，P是⊙O外一点，OP垂直于弦AB于点C，交AB弧于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB）除外：

①　　　　　　　　　　 ；②　　　　　　　 ；③　　　　　　　　　　  ；

9、如图3，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30^O，则⊙O的直径等于　　cm。

10、命题“直角都相等”的题设是　　　　　　　　 ，结论是　　　　　　 。

二、选择题：（每题3分，共9小题，满分27分）

11、中央电视台“开心辞典”栏目曾有这么一道题：圆的半径增加一倍，那么圆的面积增加了到　　　　　　　　　　　　　　　　　　　　　 （　　 ）

A、1倍　　 B、2倍　　　C、3倍　　D、4倍

12、如图4，AB=CD，BC=DA，点E、F在AC上，且AE=CF，则图中全等三角形的对数是　　　　　　　　  　　　　　　　　　　　　　　　　　　 （　 ）

A、1对　　 B、2对　　　C、3对　　　D、4对

13、已知半径为3cm和4cm的两圆外切，那么半径为6cm且与这两圆都外切的圆有　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A、1个　　 B、2个　　 C、3个　　　D、4个

14、关于x的一元二次方程一个根是0，则的值为（　）

A、1　　 B、-1　　  C、1或-1　　 D、

15、方程，配方后的结果是　　　　　　　　　　　 （　　 ）

A、　 B、　C、　D、

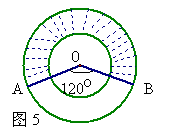
16、如图5，同心圆中，两圆半径分别为2、1，则阴影部分的面积为　（　 ）

A、　　 B、　　  C、2　　  D、4

17、一个点到圆的最小距离为4cm，最大距离为9cm，则该圆的半径是 （　　 ）

A、2.5ccm　　 B、2.5cm或6.5cm　　C、6.5cm 　　D、5cm或13cm

18、已知圆锥的母线长为6cm，底面圆的半径为3cm，则此圆锥侧面展开图的面积为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A、18cm²　　　 B、36cm²　　　　C、12cm²　　D、9cm²

19、在一副洗好的没有大小王的52张扑克牌中，闭上眼睛，随机抽出一张牌，则下列说法错误的是　　　　　　　　　　　　　　　　　　　　 （　　 ）

A、它是10的概率为　　　　　　　 B、它是方块10的概率为

C、它是红色的概率为　　　　　　  D、它是梅花的概率为

三、作图题：（本题6分）

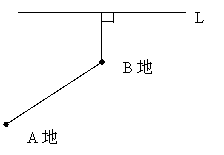
20、如图，请作出A地经过B地去河边L的最短路线。

（要求：用尺规作图，只保留作图痕迹，不写作法）

四、解答题：（本大题39分，第21题8分，第22、23题每题6分，第24题9分，第25题10分，共39分）

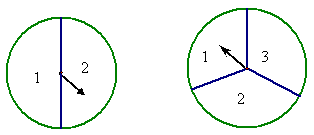
21、小明和小刚用如图的两个转盘游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分。这个游戏对双方公平吗？，若公平，说明理由。若不公平，怎样修改规则才能使游戏双方公平？

22、化简求值：其中　23、解方程：

　　　　

24、某灯具店采购了一批某种型号的节能灯，共用去400元。在搬运过程中不慎打碎了5盏，该店把余下的灯每盏加价4元全部出售，然后用所得的钱又采购了一批这种节能灯，且进价与上次相同，但购买的数量比上次多9盏，求每盏灯的进价。

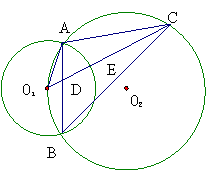25、如图，⊙O₁和⊙O₂相交于A、B两点，O₁在⊙O₂上，⊙O₂的弦O₁C分别交AB、⊙O₁于D、E，求证：（1）　 （2）E是△ABC的内心。

参考答案

一、填空题：

1、 　　2、 　　3、　　4、 4，3　 5、

6、2.5　　7、2　　 8、答案很多，如：PC⊥AB，PA=PB，∠APO=∠BPO

9、1.8　　10、直角，都相等

二、选择题：

11、D　12、C　13、B　 14、B　15、C　 16、C　 17、B　 18、A　19、A

三、作图题：

20、

四、解答题

21、不公平，两个转盘所转到的数字之积为奇数的概率为 ，两个转盘所转到的数字之积为偶数的概率为 ；

修改的方法不唯一，如：游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之和为奇数时，小明得1分；当所转到的数字之和为偶数时，小刚得1分。

22、解：原式

　　　　　　

　　　　当 时

　　　　原式

　　　　　  =

23、解：方程两边同时乘以，得

　　　　 

　　　 　　　　　　

　

经检验：　 是原2原的解

24、解：设每盏灯进价为x元，列方程得

　　　

解得：

　 　　　（不合题意，舍去）

经检验：是原方程的解

答：每盏灯进价为10元

25、证明：（1）连结O₁B　　　　　　　　　　　

　　　　　　 ∵O₁B= O₁A

∴

∴∠O₁AD= ∠O₁CA

∵∠AO₁D=∠CO₁A

∴△O₁AD ∽ △O₁CA

∴AO₁：O₁C= O₁D：AO₁

∴

（2）连结AE交O₁C于E点

∵O₁A= O₁E

∴∠O₁AE= ∠O₁EA

∵∠O₁AE= ∠O₁AD+∠DAE　　∠O₁EA=∠CAE+ ∠O₁CA

∵∠O₁AD=∠ O₁CA

∴∠DAE=∠CAE

∴AE平分∠BAC

∵

∴∠ACO₁=∠BCO₁

∴O₁C平分∠ACB

∵E点在O₁C上

∴E点是△ABC的内心

（本题证明方法多样化）