九年级单元检测
一、填空题（每小题3分，共8小题24分）
1、 关于
的一元二次方程
的一般形式是
。
2、 比较大小：
_____
； 
_____
。
3. 方程
的根是
。
4、 用配方法解方程
，则
，
所以
。
5. 当
≥
时，一元二次方程
的求根公式为
。
6、 当
时，关于
的方程
为一元二次方程。
7. 已知m是方程2x2+3x-1=0的根，求
m2+
m的值为
。
8.. 若
，
，则
=_______。
二、选择题（第小题3分，共8小题24分）
1、下面是某同学在一次数学测验中解答的填空题，其中答对的是（ ）
A、若
；
B、
；
C、
；
D、
的值为零，则
。
2、
，则
（
）
A、
B、
C、
D、
3、将方程
的形式，指出
分别是（
）
A、
B、
C、
D、
4、已知一元二次方程
，若方程有解，则必须（
）
A、
B、
C、
D、
5、若
（
）
A、
B、
C、
D、
6. 把
根号外的因式移到根号内，化简的结果是 （ ）
A 
B 
C 
D 
7、已知
，
，则下列各式中与
不相等的是 （ ）
A 
B
C 
D
8、若
，则
等于 （ ）
A 
B
C
1
D －1
三、选择适当的方法解一元二次方程（每小题4分，共16分）
1）
2）
3）
4）
三、解答题（每题6分，共36分）；
1. 若x=1是方程mx2+3x+n=0的根，求(m-n)2+4mn的值。
2. 
3. 某商场在“五一节”的假日里实行让利销售，全部商品一律按九销售，这样每天所获得的利润恰是销售收入的20%，如果第一天的销售收入4万元，且每天的销售收入都有增长，第三天的利润是1.25万元，
(1) 求第三天的销售收入是多少万元？
(2) 求第二天和第三天销售收入平均每天的增长率是多少？
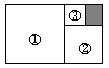
4、如图，一个长方形被分割成四部分，其中图形①、②、③都是正方形，且正方形①、②的面积分别为4和3，求图中阴影部分的面积。
5、阅读下面的例题：
解方程
解：（1）当x≥0时，原方程化为x2 – x –2=0，解得：x1=2,x2= - 1（不合题意，舍去）
（2）当x＜0时，原方程化为x2 + x –2=0，解得：x1=1,（不合题意，舍去）x2= -2∴原方程的根是x1=2, x2= - 2
（3）请参照例题解方程
6、用长20m的篱笆围成矩形，使矩形一边靠墙，另三边用篱笆围成，
⑴ 写出矩形面积S（m2）与平行于墙的一边长x（m）的关系式；并写出自变量x的取值范围
⑵ 写出矩形面积S（m2）与垂直于墙的一边长x（m）的关系式．并写出自变量x的取值范围.。