九年级数学二次函数测试卷
姓名 分数
一、 填空题（每小题3分，共21分）
1、抛物线y=－2x2－1的对称轴是 ，顶点坐标是
2、把二次函数y=－2x2＋4x+3化成y=a（x+m）2+k的形式是 ，其开口方向向
3、抛物线y=－2x2－x+3与y轴交点的坐标是 ，与x轴的交点坐标是
4、函数y=2x2的图象向左平移2个单位，再向上平移3个单位得到的函数关系式是
5、已知函数y=x2+3kx+k+1的图象过原点，那么函数的关系式是
6、请选择一组你喜欢的
的值，使二次函数
的图象同时满足下列条件：①开口向下，②当
时，
随
的增大而增大；当
时，随的增大而减小。这样的二次函数的解析式可以是
。
7、直线y=3与抛物线y=－x2+8x－12的两个交点坐标分别是A（ ）、B（ ），若抛物线y=－x2+8x－12的顶点是P，与X轴的两个交点是C、D两点，则三角形PCD的面积是
二、 选择题（每小题3分，共15分）
1、已知点（a，8）在抛物线y=ax2上，则a的值为（ ）
A、±2 B、±2
C、2
D、－2
2、二次函数y=x2＋4x＋a的最大值是2，则a的值是（ ）
A、4 B、5 C、6 D、7
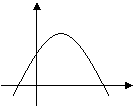
4、二次函数
的图象如图所示，则下列结论中正确的是：（ ）
|
C a<0 b>0 c<0
| |
5、下列四个函数：
① 
② 
③ 
④ 
其中，函数y的值随着x值得增大而减少的是
A、 ① B、② C、③ D、④
三、解答题（每小题6分，共18分）
1、求满足下列条件的对应的二次函数的关系式。
（1）抛物线经过（4，0），（0，－4），和（－2，3）三点。
（2）抛物线的顶点坐标是（3，—2），且经过点（5，6）。
（3）抛物线与x 轴的交点横坐标为1和5，并且经过点（0，6）。
2、已知二次函数y=－（x－4）2 +4 （本大题满分12分）
（1）、先确定其图象的开口方向，对称轴和顶点坐标，再画出草图。
（2）、观察图象确定：X取何值时，①y=0，②y﹥0，⑶y﹤0。
（3）、观察图象，可以得到二次函数的哪些性质。
3、如图，已知直线AB经过x轴上的点A（2，0），且与抛物线y=ax2 相交于B、C两点，已知B点的坐标是（1，1）。求直线和抛物线的解析式和点C 的坐标。（本大题满分10分）
4、（本大题共15分）东海体育用品商场为了推销某一运动服，先做了市场调查，得到数据如下表：（本大题满分12分）
| 卖出价格x（元/件） | 50 | 51 | 52 | 53 | …… |
| 销售量p（件） | 500 | 490 | 480 | 470 | …… |
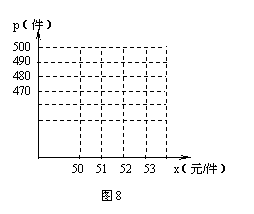
（1）以x作为点的横坐标，p作为纵坐标，把表中的
数据，在图8中的直角坐标系中描出相应的点，观察连结
各点所得的图形，判断p与x的函数关系式；
（2）如果这种运动服的买入件为每件40元，试求销售
利润y（元）与卖出价格x（元/件）的函数关系式
（销售利润=销售收入－买入支出）；
（3）在（2）的条件下，当卖出价为多少时，能获得最大利润？
5. 如图，在一块三角形区域ABC中，∠C=90°，边AC=8，BC=6，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时，水池DEFG的面积最大？
⑶实际施工时，发现在AB上距B点1.85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使三角形区域中欲建的最大矩形水池能避开大树。（本小题12分）
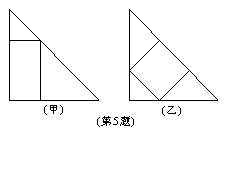
试一试：
有一张腰长为10cm的等腰直角三角形纸板, 若要从中剪一个矩形纸板, 如图所示有两种方案, 请你通过计算说出要使矩形面积最大的裁剪方案, 并指出最大面积为多少? （15分）
