九年级上第三单元检测试卷
姓名
一．选择题（每小题4分，共24分）
1．一个等腰梯形的两底之差为
，高为
，则等腰梯形的两底的一个锐角为
（ ）
A 
B 
C 
D 
2．在Rt⊿ABC中，∠ACB =
，∠A =，AC =
，则AB边上的中线为 （ ）
A 
B 
C 
D
3．等边三角形一边上高线长为
，那么这个等边三角形的中位线长为 （ ）
A 
B 
C D 
4．下列判定正确的是 （ ）
A 对角线互相垂直的四边形是菱形 B 两角相等的四边形是梯形
C 四边相等且有一个角是直角的四边形是正方形
D 两条对角线相等且互相垂直的四边形是正方形
5．顺次连结等腰梯形各边中点得到的四边形是 （ ）
A 矩形 B 菱形 C 正方形 D 平行四边形
6．直角梯形的两个直角顶点到对腰中点的距离 （ ）
A 相等 B 不相等 C 可能相等也可能不相等 D 互相垂直
二．填空题：（每小题4分，共20分）
7．已知菱形的周长为
，一条对角线长为
，则这个菱形的面积为
；
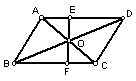8．如图：EF过平行四边形ABCD的对角线交点O，交AD于E，交
BC于F，已知AB =
，BC =
，OE =
，那么四边形EFCD的周长
为 ；
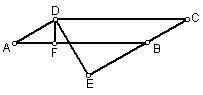9．已知，如图：平行四边形ABCD中，AB =，AB边上
的高为
，BC边上的高为，则平行四边形ABCD的
周长为 ；
10．如图，在Rt⊿ABC中，∠C =，AC = BC，AB =
，
矩形DEFG的一边在AB上，顶点G、F分别在AC、BC上，
D、E在AB上，若DG：GF =1：4，则矩形DEFG的面积
为 ；
11．在⊿ABC中，∠C =，周长为
，斜边上的中线CD =，则Rt⊿ABC的面积为
；
四．解答证明题：
12．（10分）在平行四边形ABCD中，BC = 2AB，E为BC中点，求∠AED的度数；
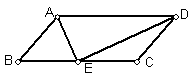
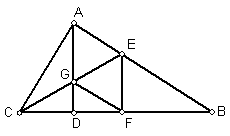13．如图：在⊿ABC中，∠BAC =，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F，求证：四边形AEFG是菱形；(10分)
14．（10分）如图，以正方形ABCD的对角线AC为一边，延长AB到E，使AE = AC，以AE为一边作菱形AEFC，若菱形的面积为
，求正方形边长；（12分）
15．如图,在等腰梯形ABCD中,AB∥CD,AC,BD是对角线,将△ABC沿AB对折到△ABE的位置.（12分）
(1) 
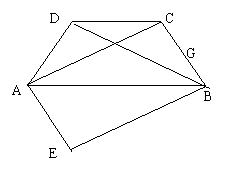度判断四边形AEBC的形状?
(2) 试证明你判断的结论.
16、已知：如图，在△ABC中，AB＝AC，AD
BC，垂足为D，AN是△ABC外角
CAM的平分线，CEAN，垂足为E，连接DE交AC于F（1）求证：四边形ADCE为矩形
（2）求证：DF∥AB，DF＝
AB
 |
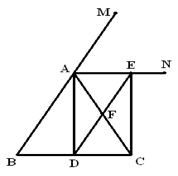（3）当△ABC满足什么条件时，四边形ADCE是一个正方形？简述你的理由。（12分）
附加题(10分)
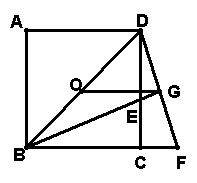
1. 已知，如图，O为正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，连接OG。
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE·GB=
，求正方形ABCD的面积。
