第一、二单元测试卷
班级：__________姓名：___________
一、选择题（每题3分，共30分）
1、已知反比例函数
的图象经过点P（—1，2），则K的值是（ ）
A、2
B、
C、—2
D、—
2、在下列函数中，y与x成反比例的是（ ）
A、
B、
C、
D、
3、抛物线
的顶点坐标是（ ）
A、（1，2） B、（—1，2） C、（1，—2） D、（—1，—2）
4、在下列函数中，函数值y随着自变量x增大而增大的是（ ）
A、
B、
C、
D、
5、如图所示，
，则反比例函数的解析式是（ ）
|
|
A、
B、
|
|
|
C、
D、
|
6、若二次函数
的图象经过原点，则m的值为（ ）
A、—1或1 B、—1 C、1 D、无法确定
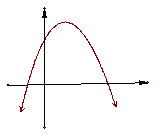
7、二次函数的图象如图所示，则下列结论正确的是（ ）
A、a>0 b<0 c>0 B、a<0 b<0 c>0
C、a<0 b>0 c>0 D、a<0 b>0 c<0
|
|
的开口方向向下，则函数
值y随自变量x的增大而减小的x的取值范围是（ ）
A、x≥3 B、x≤3 C、x≥1 D、x≤1
9、若点（—2，—3），（5，—3）在抛物线上，则该抛物线
的对称轴是直线（ ）
A、x=3 B、x= —3 C、
D、
10、抛物线
与轴交于点A、B，顶点为P，则△PAB的面积是（ ）
A、2 B、3 C、6 D、8
二、填空题（每题3分，共30分）
11、若反比例函数
经过点（1，2），请你写出另一个在该函数图象的点的坐标为____________。
12、二次函数
的对称轴是____________。
13、二次函数
，当x=_______时，函数有最_____值，值为_______。
14、已知正比例函数
与反比例函数
的图象都经过点A（m，1），则反比例函数的解析式为_____________。
15、已知
、
、
是抛物线
上的点，则___________________（比较它们的大小，并用“>”连接起来）。
16、二次函数
向左、下各平移3个单位，所得的函数解析式为___________________。
17、将函数
写成
的形式是___________________。
18、条件①对称轴为y轴 ②与坐标轴只有一个交点，请你写出满足以上条件一个函数： _______________________。
19、若二次函数
的最小值为2，则a的值为_________。
20、经市场调查，某种商品的进价为每件6元，专卖商店的每日固定成本为150元。当销售价为每件10元时，日均销售量为100件，单价每降低1元，日均销售量增加40个。设单价为x元时的日均毛利润为y元，则y关于x的函数解析式为_____________________。（只需列式）
三、解答题
21、（本题8分）已知函数
，其中
与x成正比例，
与
成反比例。当x=1时，y=1；当x=3时，y=5。试求当x=4时的值。
22、（每小题6分，本题共12分）
（1）已知抛物线经过A（—3，0），B（—1，0），C（0，3）三点，求二次函数的解析式。
（2）已知抛物线的顶点为（—1，3），且经过点（1，7），求二次函数的解析式。
23、（本题8分）经过实验获得两个变量x（x>0），y（y>0）的一组对应值如下表：
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 6 | 2.9 | 2.1 | 1.5 | 1.2 | 1 |
（1）画出相应函数的图象。
（2）求出这个函数的解析式。
（3）求当
时，x的值。
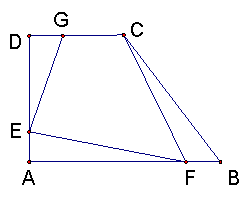
24、（本题12分）如图所示，在直角梯形ABCD中，
，截取
，已知
，
，
，求
（1）四边形CGEF的面积S关于x的函数表达式和x的取值范围。
（2）面积S是否存在最小值，若存在，求出最小值，若不存在，请说明理由。
（3）当x为何值时，S的数值等于x 的4倍。