初三上期数学期末复习题

三星初中2004－2005学年度第一学期期末复习题

初三数学综合测试

（满分：100分　　测试时间：120分钟）　　　　　　 2005年1月初使用

班级		题号	一	二	三	总分
姓名		得分

一、单项选择(每小题2分，共计12×2＝24分)

1、关于的方程有实数解，则的取值范围是（　　）

　A、＜3　　　B、≤3　　　　C、＜3　≠2　　D、≤3　≠2

2、点A（－4，1－m）关于原点对称的点在第一象限，则m的取值为（　）

A、m≠　　　　B、m<　　 　　C、m>　　 　　　　D、m=0

3、若方程的最小根的负倒数是（　　）

　A、　　　　 B、　　　　 C、　　　　　　　D、

4、若，则、的值分别为(　　)

　A、＝3　＝2　　　　　　　　B、＝2　＝3

C、＝6　＝－1　　　　　　　D、＝3　＝2或＝2　＝3

5、函数（　　）

　A、　　　　　B、　　　　　C、　　　　　　D、

6、无论（　　）象限。

　A、一　　　　　B、二　　　　　　C、三　　　　　　D、四

7、在△ABC中，∠C＝90⁰，下列各式中成立的是（　　）

　A、a=c sinB　　 B、a=bcosB　　　C、c=atanB　　　　D、a=bcotB

8、已知（　　）

　A、30⁰B、45⁰C、60⁰D、90⁰

9、⊙O的半径为4㎝，直线m上有一点A，且OA＝4㎝，则⊙O与直线m的位置关系是（　　）A、相离　　　B、相切　　　C、相交　　　D、相切或相交

10、AB、AC分别切⊙O于B、C两点，D是劣弧弧BC上的一点，若∠A＝40⁰，那么∠BDC＝（　　）A、40⁰B、80⁰C、110⁰D、70⁰

11、一直角三角形的两条直角边则它的内切圆半径的长为（　　）　　A、1　　　　B、2　　　　C、3　　　　　D、4

12、如果一次函数轴上纵坐标为2的点，则　的值为（　　）　　A、1　　　　B、3　　　　C、0　　　　　D、1或3

二、填空题(每空2分，共24分)

1、若方程＝　　　　　　。

2、在圆内接四边形ABCD中，∠A∶∠B∶∠C=2∶3∶4，则∠D= 　　　　。

3、以为根的一元二次方程可以是　　　　　　　　　　　 。

4、将二次三项式分解因式，结果为　　　　　　　　　　　　　  。

5、函数中，自变量的取值范围是　　　　　　　　　　 。

6、若一次函数的自变量的取值范围是，相应的函数值为，则该函数的解析式为　　　　　　　　　　　　　　　　　　 。

7、已知点A是的图象上的两点，且＜时，＜，则的取值范围是　　　　　　　　　 。

8、若　　　　　　　 。

9、等腰三角形的周长为，腰长为1，则该等腰三角形的底角的度数为　　 。

10、已知圆外切等梯形的中位线长为5㎝，则它的腰长为　　　　　　　 。

11、在△ABC中，AB=㎝，∠B=45⁰，∠C=60⁰，则△ABC的面积为　　　　 。

12、在同一平面内，一个圆将平面分成2(0×1+2)个部分，2个圆将平面最多分成4个(1×2+2个)部分，3个圆最多将平面分成8(2×3+2)个部分，则20个圆最多将平面分成　　　　 部分。

三、按要求解答各题(第1题每小题5分，其余各题每题7分，共52分，请注意格式)

1、解下列方程或方程组(2×5=10分) 　　

① 　　　　　　　　　② 　

　　　　　　　　　　　　　　　　　　　　　 

2、某服装店平均每天可以售出“飞鸽”牌童装20件，每件盈利40元，为了在迎接“六一”国际儿童节，该店决定采取适当的降价措施，以扩大盈利，增加售量，减少库存，经市场调查发现，每降价4元，那么平均每天可以多售出8件，要想平均每天在销售这种童装上盈利1200元，每件童装应该降价多少元？

3、某移动公司开设了两种通讯业务，“全球通”用户每月须先缴月租50元，然后每通话1分钟，再付0.2元；“神州行”用户不缴月租，每通话1分钟付0.6元，若一个月通话分钟，两种方式每月的费用为

(1)　 分别写出与之间的函数关系式；

(2)　 一个月内通话多少分钟时，两种通讯方式的费用相同？

(3)　 若某人预计一个月内使用话费120元，则应选择哪种方式？为什么？

4、已知一次函数，随的增大而减小，(1)求此函数的解析式，并画出函数图象；(2)求此函数的图象与坐标轴所围成的三角形的面积。

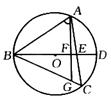
5、如图⊙O的弦AB和CD的延长线相交于点E，请根据以上条件，写出一个正确的结论，(所写结论不能再添加新的线段和标注其它字母)；并给出证明(证明时允许自行添加辅助线)。

6、将水库拦水坝背水坡坝顶加宽2米，坡度由原来的1:2改为1:2.5，已知：坝高6米，坝长50米。求加宽部分横断面AEFB的面积；计算完成这一工程需要多少土方？

7、如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连结OD，且∠AOD=∠APC.

①求证：AP是⊙O的切线；

②若OC：CB=1：2，且AB=9，求sinA的值及⊙O的面积.

附加题(每做对一道可奖励3分，自行添加答题纸)

1、阅读：“方程的解是；方程的解是；

……”①观察上述方程及其解，猜想关于x的方程的解；并利用解方程验证。

②用你猜想的结论解方程.

2、m为何值时？方程的两根分别是一个直角三角形两锐角的正弦。

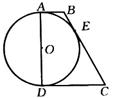3、已知：直角梯形ABCD，AB∥DC，AD⊥DC，AD=12，以AD为直径的⊙O切BC于E点，AB=x，DC=y.（1）写出y与x的函数关系式；（2）若x，y为方程两根，求梯形ABCD的面积.

4、已知：⊙O内接△ABC中，直径BD交AC于E，AF⊥BD于F，延长AF交BC于G。

求证：AB²=BG•BC.