2006年临海中学第一次统练数学试题
亲爱的同学：
欢迎参加生动活泼，意味无穷的数学“旅行”．相信聪明的你一定会认真细致地克服“旅行”中的一些小小困难，顺利到达目的地．“旅行”中请注意：全卷共三大题，满分150分，考试时间120分钟.请直接在试卷上书写答案.
一、选择题（本题有12小题，每小题4分，共48分．每小题有且只有一个选项是正确的，不选、多选、错选均不给分）
1．2的倒数是（ ）
(A) －2 (B) 1/2 (C) －1/2 (D) 1
2．下列方程，是一元二次方程的是（ ）
①3x2+x=20，②2x2-3xy+4=0，③x2-
=4，④x2=0，⑤x2-
+3=0
A．①② B．①②④⑤ C．①③④ D．①④⑤
3．若反比例函数
的图象经过(－2, 1 )，则k的值为 (
)
(A)－2
(B) 2
(C) －
(D)
4．下列计算正确的是 ( )
（A）3x－2x＝1 （B）3x+2x=5x2 (C) 3x·2x=6x (D) 3x－2x=x
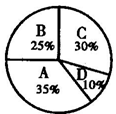5．下图所示的扇形图是对某班学生知道父母生日情况的调查，A表示只知道父亲生日，B表示只知道母亲生日，C表示知道父母两人的生日，D表示都不知道．若该班有40名学生，则知道母亲生日的人数有（ ）
A．25% B．10 C．22 D．12
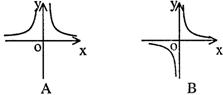
6．如果矩形的面积为6cm2，那么它的长y cm与宽x cm之间的函数关系用图象表示大致
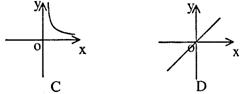
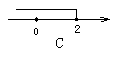
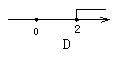
7．不等式2x＞4的解集在数轴上表示为( )
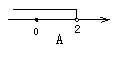
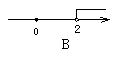
8．要使根式
有意义,则字母x的取值范围是( )
(A) x≥3 (B) x＞3 (C) x≤3 (D) x≠3
9．在三边分别为下列长度的三角形中，哪些不是直角三角形（ ）
A、5，13，12 B、2，3，
C、4，7，5 D、1，
，
10.分式
的值等于0，则x的值为( )
A．1 B．±1 C． D．－1
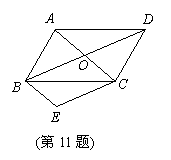11．如图，平行四边形ABCD中，对角线AC，BD
相交于点O，将△AOD平移至△BEC的位置，
则图中与OA相等的其它线段有( )
(A)1条 (B)2条
(C)3条 (D)4条
12.小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是 （ ）
二、填空题（本题有8小题,每小题4分,共32分）
13．分解因式：x2－4 =_____________________________．
14．化简
=________．
15．x2-10x+________=（x-________）2．
16．已知数据：1，2，1，0，－1，－2，0，－1，这组数据的方差为 .
17已知菱形的两条对角线长为12cm和6cm，那么这个菱形的面积
为
cm2.
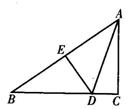
18．如图，在△ABC中，∠C=90°，AB的垂直平分线交BC于点D，如果∠CAD=20°，则∠B=_______．
19．日常生活中，“老人”是一个模糊概念．有人想用“老人系数”来表示一个人的老年化程度．他设想“老人系数”的计算方法如下表：
| 人的年龄x（岁） | x≤60 | 60＜x＜80 | x≥80 |
| 该人的“老人系数” | 0 |
| 1 |
按照这样的规定，一个70岁的人的“老人系数”为 ．
20．下面是一组按规律排列的数：1，2，4，8，16，……，则第2005个数是 .
三、解答题（本题有7小题，共70分，须写出解答与推理的过程）
21．（本小题8分） 计算： 
(3－π)0．
．
22. （本小题8分）解方程：
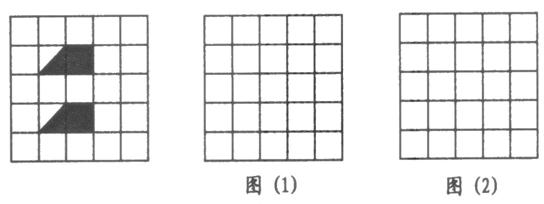
23．（本小题8分）如图，在网格中有两个全等的图形(阴影部分)，用这两个图形拼成轴对称图形，试分别在图(1)、(2)中画出两种不同的拼法．
24.（10分）2006年世界杯足球赛的揭幕战于北京时间6月10日凌晨0：00在德国慕尼黑安联球场进行，由东道主德国队对阵哥斯达黎加队，最终是德国队以4：2的比分战胜哥斯达黎加队获得首场比赛的胜利场比赛中德国队的首发阵容名单和他们的身高如下表：（单位：米）
| 姓名 | 莱曼 | 拉姆 | 梅策尔德 | 弗里德里希 | 博罗夫斯斟 | 弗林斯 |
| 身高 | 1.90 | 1.70 | 1.93 | 1.90 | 1.94 | 1.82 |
| 姓名 | 施奈德 | 克洛斯 | 默特萨克 | 波多尔斯基 | 施魏因斯斯泰格 | |
| 身高 | 1.76 | 1.82 | 1.96 | 1.75 | 1.86 |
请你求出这些运动员身高的众数、中位数和平均数（精确到0.01）
25．（12分）某商厦今年一月份销售额为60万元，二月份由于种种原因，经营不善，销售额下降10%，以后加强改进管理，经减员增效，大大激发了全体员工的积极性，月销售额大幅度上升，到四月份销售额猛增到96万元，求三、四月份平均每月增长的百分率是多少？（精确到0．1%）
26．（本小题12分）
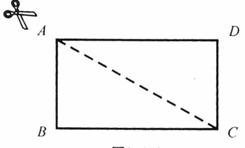
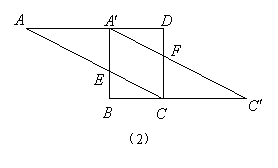
将下图（1）中的矩形
沿对角线
剪开，再把
沿着
方向平移，得到图（2）中的
，除
与
全等外，你还可以指出哪几对全等的三角形（不能添加辅助线和字母）？请选择其中一对加以证明．
| |||
 | |||
(1)
27. （本小题12分）已知直线
和直线
相交于C点，且与
轴分别相交于点
，
，且
是方程
的两个实数根．
(1)分别求出点A和点B的坐标。
（2）分别求出直线和
的解析式；
（3）求△ABC的面积；
（4）在轴上是否存在点
，使得△OCP为等腰三角形？若存在，求出点的坐标；若不存在，说明理由．
