温州市部分中学2004学年第一学期期中考试
初三数学试题卷
 一、填空题(每小题3分,共24分)
一、填空题(每小题3分,共24分)
1.
化简:![]() = 。
= 。
2. 在实数范围内因式分解:2x2-1=___________________。
3.
已知方程x2+mx+n=0和方程(x-3)(x+2)=0的解相同,求![]() =______________。
=______________。
4.
方程![]() 的解是___________________。
的解是___________________。
5.
![]()
 抛物线y= -5(x+3)2+2的顶点坐标是
对称轴是直线__________。
抛物线y= -5(x+3)2+2的顶点坐标是
对称轴是直线__________。
6.
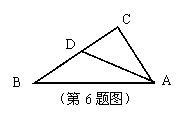
![]() 如图∠CAD=∠B,AC=6,DC=4,则BD= 。
如图∠CAD=∠B,AC=6,DC=4,则BD= 。
7. 把长为8cm的线段黄金分割,则较长线段的长
等于 cm 。
8. 下列每个图是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案的花盆的总数是S



n=2 ,S=3 n=3, S=6 n=4, S=9
按此规律推断,S与n的关系式为 。
二、 选择题(每小题3分,共24分)
9.使![]() 在实数范围内有意义,则a的取值范围为………………………( )
在实数范围内有意义,则a的取值范围为………………………( )
A、a为任何实数
B、![]()
C、![]() D、
D、![]()
10、下列x,y的值不是二元二次方程![]() 的解是……( )
的解是……( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、把![]() 的图像向右平移
的图像向右平移![]() 个单位,再向下平移1个单位,则所得图像表示的函数是…………………………………………………………………( )
个单位,再向下平移1个单位,则所得图像表示的函数是…………………………………………………………………( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
12、已知![]() ,
,![]() 的第四比例项是………………………( )
的第四比例项是………………………( )
A、2.5 B、7.5 C、10 D、3
13、已知![]() ,则
,则![]() 的值是……………………………( )
的值是……………………………( )
A、1 B、0 C、—1 D、不确定
|
|
|
 A、
A、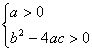 B、
B、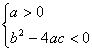
|
|
|
|
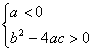 D、
D、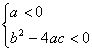
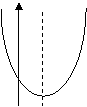
15、如图,△ABC中,D,E,F分别是BC,AB,AC边上的点,且DE∥AC,
|
|
|
 A、
A、![]()
![]()
![]() C、
C、![]() D、
D、![]()
|
![]() 16、已知二次函数
16、已知二次函数![]() 的图象如图所示,则下列结论
的图象如图所示,则下列结论
(1)![]() (2)
(2)![]() 的两根之和为正
的两根之和为正
(3)![]() ,(4)
,(4)![]() ,其中正确的结论有几个……(
)
,其中正确的结论有几个……(
)
A、1 B、2 C、3 D、4
三、解答题(第17、18、19、20题每题5分,第21、22题7分,共32分)
![]() 17 .(本题5分) 计算:
17 .(本题5分) 计算: ![]()
18.(本题5分)解方程:![]()
19.(本题5分).解方程租: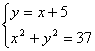
20.(本题5分)求作一个一元二次方程,使它的两根是方程![]() 的
的
两根的相反数
21.已知二次函数![]()
(1)(本题5分)证明不论m为何实数,二次函数的图象与x轴总有两个交点。
(2)(本题2分)当函数图象经过点(3,6)时,确定m的值。
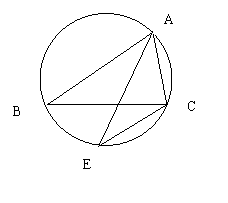
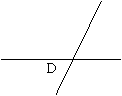
22.(本题7分)如图,△ABC中,∠BAC的平分线交BC于点D,
交△ABC的外接圆于点E.
![]()
![]() 求证:AB AC=AD AE
求证:AB AC=AD AE
|
四、解答题(第23题8分,第24题10分)
23. 关于![]() 的方程
的方程![]()
(1) (本题2分)求方程的两根和,两根积 (用k的代数式来表示)
(2) (本题6分)是否存在负数![]() ,使方程的两个实数根的倒数和为
,使方程的两个实数根的倒数和为![]() ?若存在,求出满足条件的负数
?若存在,求出满足条件的负数![]() 值,若不存在,请说明理由?
值,若不存在,请说明理由?
24.温州某瓜果基地市场部小王为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两方面的信息,如甲、乙两图
|
| ||||||||||


| | |||||||||
![]()
![]()
![]()
![]()
![]()
|
|
|
|
![]()
|
![]() 注:甲、乙两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低;甲图的图象是线段,乙图的图象是抛物线段。
注:甲、乙两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低;甲图的图象是线段,乙图的图象是抛物线段。
现在请你根据提供的信息来说明:
(1)(本题2分)3月份出售这种蔬菜,每千克的利润是多少元?(利润=售价—成本)
(2)(本题8分)哪个月份出售这种蔬菜,每千克的利润最大?并求该月每千克的最大利润?
温州市部分中学2004学年第一学期期中考试
初三数学答案
一、填空题
1、![]() 2、
2、![]() 3、6
3、6
4、![]() 5、(-3,2),
5、(-3,2),![]() 6、5
6、5
7、![]() 8、
8、![]()
二、选择题
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | B | D | A | C | C | B | B | C |
三、
17、![]()
![]() (3分)
(3分)
![]() (2分)
(2分)
18、解:设![]()
则原方程化为![]() (1分) 解得
(1分) 解得![]() (1分)
(1分)
当![]() 时,
时,![]() ,∴
,∴![]() (1分)
(1分)
当![]() 时,
时,![]() 无解 (1分)
无解 (1分)
|
|
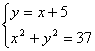
解:把(1)代入(2)得![]()
整理,得![]() (1分)
(1分)
解这个方程得![]() (1分)
(1分)
把![]() 代入(1),得
代入(1),得![]() (1分)
(1分)
把![]() 代入(1),得
代入(1),得![]() (1分)
(1分)
所以原方程组的解是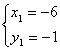 ,
,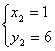 (1分)
(1分)
20、设方程![]() 的两根为
的两根为![]() ,
,
则所求的方程两根记为![]() (1分)
(1分)
由韦达定理知![]()
![]() (1分)
(1分)
则![]()
![]() (1分)
(1分)
所以所求一元二次方程为:![]() (2分)
(2分)
(方法不唯一,答案不唯一,![]() 均可,
均可,![]() )
)
21、解:(1)△=![]() (1分)
(1分)
![]()
![]() (1分)
(1分)
∵m无论为何实数,![]()
∴![]() 即△>0 (2分)
即△>0 (2分)
∴不论m为何实数,二次函数与x轴有两个交点。(1分)
(2)把(3,6)代入![]() (1分)
(1分)
则![]() 即
即![]() (1分)
(1分)
22、证明:∵AE为∠BAC的平分线,∴∠BAD=∠EAC (1分)
又∵∠B=∠E (1分)∴△ABD∽△AEC (2分)
∴![]() (2分)
(2分)
即AB·AC=AD·AE (1分)
23、(1)设方程的两根为![]() ,则由韦达定理知
,则由韦达定理知![]() (1分)
(1分)
![]() (1分)
(1分)
(2)∵![]() (1分)
(1分)
∴![]() ,即
,即![]()
整理得![]() (1分)
∴
(1分)
∴![]() (1分)
(1分)
当![]() 时,△
时,△![]() (2分)
(2分)
∴不存在负数![]() ,使方程的两实数根的倒数和为
,使方程的两实数根的倒数和为![]() 。(1分)
。(1分)
24、(1)由图可知,3月份成本是4元,售价是5元,所以在3月份出售这种蔬菜,每千克的利润是1元。(2分)
(2)由甲图可知每千克售价与月份的关系式为:![]()
把(3,5),(6,3)代入得![]() 解得
解得![]()
∴![]() (2分)
(2分)
由乙图可知每千克成本与月份的关系式为:![]() ,顶点为(6,1)
,顶点为(6,1)
则![]() ,把(3,4)代入得
,把(3,4)代入得![]() ∴
∴![]() (2分),
(2分),
设每千克的利润为y元,月份为x,则![]() (1分)
(1分)
整理得![]() (1分)∴当
(1分)∴当![]() ,
,![]() 元(2分)
元(2分)
答:在5月份出售这种蔬菜,每千克的利润最大,最大值为![]() 天。
天。