二次根式的性质(含答案)

二次根式的性质专题训练题

1．当x=________时，代数式9-有最大值，其最大值为_______．

2．当x=________时，代数式有最小值，其最小值为_______．

3．如果等式=-a成立，则字母a的取值范围是_______．

4．若等式=-x成立，那么a的取值范围是_______，x的取值范围是________．

5．把式子（x-1）中根号外的因式移到根号内，结果是________．

6．若+=3，则x的取值范围是________．

7．已知a、y均为实数，且满足等式y=，试求y²⁰⁰⁶的个位数字．

8．若x、y均为实数，且满足等式

+=·，求a的值．

9．请你先计算=________；=_______；=________，从而发现规律．求的值（n是自然数，n≥1）．

答案:

1．3；9　点拨：根据二次根式的性质，≥0，

所以当x=3时，的最小值为0，9是一个定值，

所以减数越小，其差就越大，

所以当x=3时，9-可取得最大值9．

2．-；-3　点拨：由于≥0，

所以的最小值为0，这时x的值是-，

由于式子中减数是固定不变的，差随被减数的减小而减小，

故当x=-时，的最小值是0，式子的最小值是0-3=-3．

3．-1≤a≤0　点拨：解法一：因为==-a，

所以│a│=-a，a+1≥0，-1≤a≤0．

解法二：根据二次根式的非负性，≥0，≥0，

所以-a≥0，-1≤a≤0．

4．a≥0；x≤0　点拨：因为==·=·x=-x．

　　所以-x≥0，所以x≤0，因为-ax≥0，所以a≥0．

5．-　点拨：因为≥0，所以x<1，即x-1<0．

　　所以（x-1）=-（1-x）=-=-．

　　欲把根号外的因式移到根号内，首先必须弄清题中x的取值范围，由二次根式的定义，就可得x<1．其次，移到根号内的因式必须是非负数，才能保证变形的恒等性，否则会发生符号错误．

6．5≤x≤8　点拨：+=│x-5│+│x-8│．

　　当x<5时，x-5<0，x-8<0，

　　所以原式=5-x+8-x=13-2x．

　　当5≤x≤8时，x-5≥0，x-8≤0．

　　所以原式=x-5+8-x=3，

　　当x>8时，x-5>0，x-8>0，

　　所以原式=x-5+x-8=2x-13．

　　所以x的取值范围是5≤x≤8．

　　欲化去题目中出现的绝对值，必须依题意弄清（x-5）与（x-8）的符号，而题目中的条件不足以说明这两个式子的符号，故采用了上述对数轴进行分段讨论的方法，这种方法又叫做零点取值法，通过对各种情况的分析讨论，最终得到正确答案．

7．解：依题意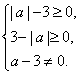 解得a=-3，所以y==-2．

　  所以y²⁰⁰⁶=（-2）²⁰⁰⁶=2²⁰⁰⁶=2²⁰⁰⁴×2²．

　　因为2¹=2，2²=4，2³=8，2⁴=16．

　　2⁵=32，2⁶=64，2⁷=128，2⁸=256．

　　所以2²⁰⁰⁴的个位数一定是6，2²⁰⁰⁶的个位数一定是4．

　　点拨：由二次根式的定义及分式的定义，求出a的值为-3是解题的关键，在y=-2的基础上，求（-2²⁰⁰⁶）的个位数字，需要一定的观察、推理和归纳能力，通过几个简单数字的计算，知道了2ⁿ的个位数字是以4个数为一个循环，即从2¹开始到2⁴为一个循环，个位数字依次是2、4、6、8，依此类推，到2²⁰⁰⁴时正好是501个循环，2²⁰⁰⁶是第502个循环的第二个数，故个位数字是4．

8．解：依题意： 解得x+y=199 ①

　　即+=0

　　由非负数的性质可知：3x+5y-2=0 ②

　  2x+4y-a=0　③

　　由②-①得，2x+4y=-197　④

　　④-③得，a=-197．

　　点拨：从观察等式右边的两个二次根式的被开方数入手，由于x-199+y与199-x-y互为相反数且均为非负数，故x+y的值必为199，再由二次根式的非负性及非负数的性质可知3x+5y-2=0且2x+4y-a=0，然后用整体加减的办法求出2x+4y的值，也可以由①②组成二元一次方程组，求出x、y的值，再代入③，即可求出a的值．

9．3；33；333；=

　　点拨：先认真计算每一个二次根式的结果，然后通过观察，分析推理，即可得出结论，被开方数中被减数每个数位上都是1，减数每个数位上都是2，被减数的位数是减数位数的2倍，化简的结果每个数位上都是3，位数与减数相同．