初 三 数 学 模 拟 试 卷 (2006.1 )
一、 细心填一填：（本大题有12小题，共15空，每空2分，满分30分。请把结果直接填在题中的横线上。只要你理解概念，仔细运算，相信你一定会填对的！）
1．－3的相反数是 ；4的算术平方根是 。
2．太阳的直径约为米，用科学记数法可表示为 。（保留两个有效数字）
3．函数
中自变量
的取值范围是 ；
中自变量的取值范围是 。
4．设
是方程
的两个实数根。则
=
。
5．把二次函数
的图象沿轴向右平移3个单位，沿
轴向下平移2个单位，则平移后的图象所表示的函数解析式是
。
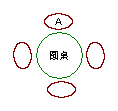
6. 一张圆桌旁有四个座位，A先坐在如图所示的座位上，B、C、D三
人随机坐到其他三个座位上。则A与B不相邻而坐的概率是 。
7．若关于x的方程x2+2(k-1)x+k2=0有实数根，则k的取值范围是
8．若方程
有增根，则它的增根是 .
9、直线
与轴、轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在轴上的点
处，则直线AM的解析式为 。
10．如图是一棵美丽的“勾股树”，它所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为10㎝，则正方形
的面积和=
㎝
。
11.如图，时钟的钟面上标有1，2，3,……，12共12个数，一条直线把钟面分成了两部分.请你再用一条直线分割钟面，使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等，则其中的两个部分所包含的几个数分别是 和. 。
12．如图8，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米(左右对称)，则该秋千所荡过的圆弧长 (精确到0.1米)。
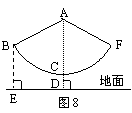
（第10题） （第12题）
二、 精心选一选：（本大题有8小题，每小题3分，满分24分。在每题所给出的四个选项中，只有一项是符合题意的。把所选项前的字母代号填在题后的括号内。只要你掌握概念，认真思考，相信你一定会选对！）
13．下列运算正确的是 （ ）
.
.
.
.
14．从根的情况判断，下列哪个方程与其它三个不同？ ( )
.
.
. 
.
15．小丽制作了一个对面图案均相同的正方体礼品盒（如下左图所示），则这个正方体礼品盒的平面展开图可能是 （ ）．
A
B
C
D
16．图中的
是由矩形纸片
沿对角线
折叠而得到，图中（包括实线、虚线在内）共有全等三角形（ ）
.2对 .3对 . 4对 .5对
17.在长度分别是3，4，8的三条线段中，任取两条线段作两圆的半径，第三条线段作圆心距，则两圆的位置关系是………………………………………………………（ ）
A、外离或相交 B、内含或相交 C、外离或内含 D、外离或内含或相交
18．若圆锥的轴截面是一个边长为2cm的等边三角形,则这个圆锥的侧面积是 ( )
A、
B、
C、
D、
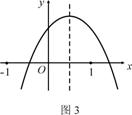
19．已知二次函数y=ax2+bx+c(a≠0)的图象如图3所示，给出以下结论：① a+b+c<0；② a-b+c<0；③ b+2a<0；④ abc>0 . 其中所有正确结论的序号是 ( )
A. ③④ B. ②③ C. ①④ D. ①②③
20.某校数学课外活动探究小组，在老师的引导下进一步研究了完全平方公式．结合实
数的性质发现以下规律：对于任意正数a、b， 都有a+b≥2
成立．
某同学在做一 个面积为3 600cm2，对角线相互垂直的四边形风筝时，运用上述
规律，求得用来做对角线用的竹条至少需要准备xcm． 则x的值是 ( )
(A) 120
(B)
60
(C) 120
(D) 60
三．认真答一答（本大题共有8小题，满分58分。只要你仔细审题，积极思考，一定会解答正确的！）
21．（本题共有2小题，每小题4分，共8分）
(1)计算： (
)0+(
)-1-
--1 (2)解方程
22．(本小题4分)先化简，再请你用喜爱的数代入求值:
.
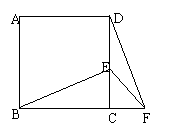
23．（本题满分8分）已知：如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，且CE=CF，
⑴求证：△BCE≌△DCF；
⑵若∠FDC=30°，求∠BEF的度数.
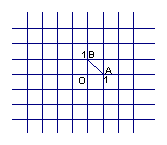
24．（6分）如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心。此时，M是线段PQ的中点。 如图，在直角坐标系中，⊿ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0）。点列P1、P2、P3、…中的相邻两点都关于⊿ABO的一个顶点对称：
点P1与点P2关于点A对称，点P2与点P3关于点B对称，
点P3与P4关于点O对称，点P4与点P5关于点A对称，点P5
与点P6关于点B对称，点P6与点P7关于点O对称，…。对称
中心分别是A、B，O，A，B，O，…，且这些对称中心依次循环。已知点P1的坐标
是（1，1），试求出点P2、P7、P100的坐标。
P2( ) 、 P7( ) 、 P100 ( )
25.（8分）如图，已知直线
与轴、轴分别交于点A、B，与双曲线
（<0）分别交于点C、D，且C点的坐标为（
，2）.
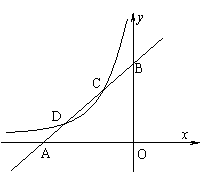⑴分别求出直线AB及双曲线的解析式；
⑵求出点D的坐标；
⑶利用图象直接写出：当x在什么范围内取值时，
>
.
26．（本题满分8分）．某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．
(1) 写出所有选购方案(利用树状图或列表方法表示)；
(2) 如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．
27.（本题满分8分）
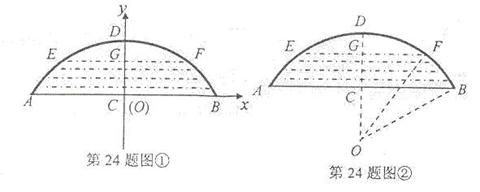
一座拱型桥，桥下的水面宽度AB是20米，拱高CD是4米.若水面上升3米至EF，则水面宽度EF为多少？
（1）若把它看作抛物线的一部分，在坐标系中（如图①），可设抛物线的表达式为
请你填空： a= ,c=
,EF= 米
（2）若把它看作圆的一部分，可构造图形（如图②）请估计（2）中EF与（1）中你计算出的EF的差的近似值（误差小于0.1米）
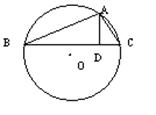
28．（本题满分8分）如图，已知在⊙O的内接△ABC中，AB+AC=12，AD⊥BC于D，AD=3，设⊙O的半径为y，AB的长为x.
(1)求y与x的函数关系式；
(2)当AB的长为多少时,⊙O的面积最大?并求出⊙O的最大面积.
四、动脑想一想（本大题共有2小题，满分18分。开动你的脑筋，只要你勇于探索，大胆实践，你一定会获得成功的！）
29．（本题满分9分）．等腰△ABC，AB=AC=８，∠BAC=120°，P为BC的中点，小慧拿着含300角的透明三角板，使300角的顶点落在点P，三角板绕P点旋转．
（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE～△CFP；
（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
① 探究１：△BPE与△CFP还相似吗？（只需写出结论）
② 探究２：连结EF，△BPE与△PFE是否相似？请说明理由；
③ 设EF=m，△EPF的面积为S，试用m的代数式表示S．
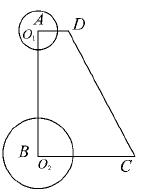
29．（本题满分9分）如图,已知直角梯形ABCD中，AD∥BC，∠A=90o，∠C=60o，AD=3cm，BC=9cm．⊙O1的圆心O1从点A开始沿A—D—C折线以1cm/s的速度向点C运动，⊙O2的圆心O2从点B开始沿BA边以
cm/s的速度向点A运动，如果⊙O1半径为2cm，⊙O2的半径为4cm，若O1、O2分别从点A、点B同时出发，运动的时间为ts
（1）请求出⊙O2与腰CD相切时t的值；
（2）在0s<t≤3s范围内，当t为何值时，⊙O1与⊙O2外切？
